Course Standards
General Course Information and Notes
General Notes
Access courses are intended only for students with a significant cognitive disability. Access courses are designed to provide students with access to the general curriculum. Access points reflect increasing levels of complexity and depth of knowledge aligned with grade-level expectations. The access points included in access courses are intentionally designed to foster high expectations for students with significant cognitive disabilities.
Access points in the subject areas of science, social studies, art, dance, physical education, theatre, and health provide tiered access to the general curriculum through three levels of access points (Participatory, Supported, and Independent). Access points in English language arts and mathematics do not contain these tiers, but contain Essential Understandings (or EUs). EUs consist of skills at varying levels of complexity and are a resource when planning for instruction.
English Language Development ELD Standards Special Notes Section:
Teachers are required to provide listening, speaking, reading and writing instruction that allows English language learners (ELL) to communicate information, ideas and concepts for academic success in the content area of Mathematics. For the given level of English language proficiency and with visual, graphic, or interactive support, students will interact with grade level words, expressions, sentences and discourse to process or produce language necessary for academic success. The ELD standard should specify a relevant content area concept or topic of study chosen by curriculum developers and teachers which maximizes an ELL’s need for communication and social skills. To access an ELL supporting document which delineates performance definitions and descriptors, please click on the following link: https://cpalmsmediaprod.blob.core.windows.net/uploads/docs/standards/eld/ma.pdf.
General Information
- Class Size Core Required
Educator Certifications
Student Resources
Original Student Tutorials
Identify and classify quadrilaterals, including squares, rectangles, and rhombi, using their defining attributes in tables and Venn diagrams with this interactive tutorial.
Type: Original Student Tutorial
By the end of this tutorial you should be able to identify examples of quadrilaterals and their defining attributes to classify them using diagrams. We will focus on kites and other quadrilaterals in this tutorial.
This part 7 in a 8-part series. Click below to explore the other tutorials in the series.
Part 1: "Figuring Out" 2D Figures
Part 2: Exploring Relationships with Venn & Euler Diagrams
Part 3: Classifying Triangles by Angles Using Euler Diagrams
Part 4: Classifying Triangles by Sides & Angles Using Venn and Euler Diagrams
Part 5: Quadrilaterals
Part 6: Trapezoids
Part 8: (Coming Soon)
Type: Original Student Tutorial
Join Party On Productions to solve whole number division problems with remainders using the partial quotient method in this interactive tutorial.
Type: Original Student Tutorial
Learn to divide whole numbers by unit fractions as you help Allie and Cameron create equal shares of candy and prizes for guests at a carnival in this interactive tutorial.
Type: Original Student Tutorial
Solve real-world word problems involving dividing a unit fraction by a whole number and dividing a whole number by a unit fraction using number lines in this chocolate-themed, interactive tutorial.
This is part 2 of a 2-part series. Click HERE to open "Chocolate Shop Challenge Part 1: Dividing Unit Fractions and Whole Numbers Using Fraction Bar Models"
Click HERE to open the related tutorial, "David Divides Desserts: Divide a Unit Fraction by a Whole Number"
Type: Original Student Tutorial
Divide unit fractions by whole numbers and divide whole numbers by unit fractions in this chocolate-themed, interactive tutorial.
This is part 1 of a 2-part series. Click HERE to open "Chocolate Shop Challenge Part 2: Dividing Unit Fractions and Whole Numbers Using Number Lines"
Type: Original Student Tutorial
Learn to solve word problems involving division of a unit fraction by a whole number by using models, expressions, equations, and strategic thinking in this interactive, dessert-themed tutorial.
Type: Original Student Tutorial
Learn how to divide a unit fraction by a whole number to share yummy picnic goodies equally in this interactive tutorial.
Type: Original Student Tutorial
Learn to solve addition and subtraction word problems involving fractions with unlike denominators. As you complete this art-themed, interactive tutorial, you'll use visual models, write and solve equations, and check the reasonableness of results based on estimates.
This is part 2 of a two-part series. Click below to open part 1.
Type: Original Student Tutorial
Read word problems and use number lines with benchmarks to solve multi-step problems involving addition and subtraction of fractions with unlike denominators. In this tutorial, you will help Daisy and Angie paint pictures using fractions.
Type: Original Student Tutorial
Explore the defining attributes of trapezoids--a special type of quadrilateral--and classify them using diagrams in this interactive tutorial. You'll also learn how two different definitions for a trapezoid can change affect classifications of quadrilaterals.
This part 6 in a 6-part series. Click below to explore the other tutorials in the series.
Part 1: "Figuring Out" 2D Figures
Part 2: Exploring Relationships with Venn & Euler Diagrams
Part 3: Classifying Triangles by Angles Using Euler Diagrams
Part 4: Classifying Triangles by Sides & Angles Using Venn and Euler Diagrams
Type: Original Student Tutorial
Explore rounding decimals through the thousandths place as you help Tyrese the Turtle train to race the hare in this interactive tutorial.
Type: Original Student Tutorial
Learn how to convert time from seconds to minutes, minutes to hours, and hours to days. In this interactive tutorial, you will also practice converting time to fractional amounts.
Type: Original Student Tutorial
Help out at the fishing tournament while comparing decimals through the thousandths place in this interactive tutorial.
Type: Original Student Tutorial
Help Buffy multiply fractions by whole numbers using the standard algorithm in addition to visual fraction models in this bakery-themed, interactive tutorial.
This is part 4 of a 4-part series. Click below to open other tutorials in the series.
Type: Original Student Tutorial
Help Buffy the Baker multiply a fraction by a whole using models in this sweet interactive tutorial.
This is part 3 of a 4-part series. Click below to open other tutorials in the series.
Type: Original Student Tutorial
Help Buffy the Baker multiply fractions less than one by relating the standard algorithm to visual models as he runs his bakery in this interactive tutorial.
This is part 2 of a 4-part series. Click below to open other tutorials in the series.
Type: Original Student Tutorial
Explore how to add fractions less than one with unlike denominators in this magical, interactive tutorial.
Type: Original Student Tutorial
Help Buffy the Baker use visual models to multiply fractions less than one as he runs his bakery in this interactive tutorial.
This is part 1 of a 4-part series. Click below to open other tutorials in the series.
- Part 2: Multiplying Fractions
- Part 3 Using Models to Multiply a Fraction by a Whole Number
- Part 4: Multiplying a Fraction by a Whole Number - Standard Algorithm
Type: Original Student Tutorial
Learn why it's sometimes important to use social distancing to reduce the spread of germs and how to estimate and convert this customary distance with this interactive tutorial.
Type: Original Student Tutorial
Help build a Grasshopper Hut for Gus by creating line plots and answering questions about the line plots in this interactive tutorial.
Type: Original Student Tutorial
Help solve the problem of shipping video games and accessories to customers by calculating the volume of the containers needed in this interactive tutorial.
Type: Original Student Tutorial
Build on your previous knowledge of area and learn how to calculate volume in cubic units with this interactive tutorial.
Type: Original Student Tutorial
Explore base 10 and exponents in this baseball-themed, interactive tutorial.
Type: Original Student Tutorial
Help your town build a dog park by multiplying whole numbers by decimals to the tenths place in this interactive tutorial.
Note: this is an introductory tutorial on multiplying whole numbers by decimals before students move on to multiplying decimals by decimals.
Type: Original Student Tutorial
Learn to subtract decimals to the hundredths place using place-value models and written expressions as you fix the topsy-turvy playground in this interactive tutorial.
Type: Original Student Tutorial
Help these aliens clean up the Sweet Treats Factory by learning to add decimals in this interactive mathematics tutorial.
Type: Original Student Tutorial
Learn how to show relationships represented in Venn & Euler Diagrams as you complete this interactive geometry tutorial.
This is part two of four. Click below to open the other tutorials in the series.
- Part 1: "Figuring Out" 2D Figures - Part 1
- Part 2 Exploring Relationships with Venn & Euler Diagrams
- Part 3: Classifying Triangles by Angles using Euler Diagrams
- Part 4: Classifying Triangles by Sides and Angles using Venn and Euler Diagrams
Type: Original Student Tutorial
Learn how triangles can be sorted and classified using side lengths and angle measures in this interactive tutorial.
This is the final tutorial in a four-part series. Click below to open the other tutorials in the series.
- Part 1: "Figuring Out" 2D Figures - Part 1
- Part 2 Exploring Relationships with Venn & Euler Diagrams
- Part 3: Classifying Triangles by Angles using Euler Diagrams
- Part 4: Classifying Triangles by Sides and Angles using Venn and Euler Diagrams
Type: Original Student Tutorial
Try to escape from this room using multiplication as scaling in this interactive tutorial.
Note: this tutorial is an introductory lesson on multiplying a given number without calculating before working with fractions.
Type: Original Student Tutorial
Learn to classify triangles and use Euler diagrams to show relationships, in this interactive tutorial.
This is part-three of four. Click below to open the other tutorials in the series.
- Part 1: "Figuring Out" 2D Figures - Part 1
- Part 2 Exploring Relationships with Venn & Euler Diagrams
- Part 3: Classifying Triangles by Angles using Euler Diagrams
- Part 4: Classifying Triangles by Sides and Angles using Venn and Euler Diagrams
Type: Original Student Tutorial
Explore 2D (two-dimensional) figures and see how every 2D figure possesses unique attributes in this interactive tutorial.
This is part one of four. Click below to open the other tutorials in the series.
- Part 1: "Figuring Out" 2D Figures - Part 1
- Part 2 Exploring Relationships with Venn & Euler Diagrams
- Part 3: Classifying Triangles by Angles using Euler Diagrams
- Part 4: Classifying Triangles by Sides and Angles using Venn and Euler Diagrams
Type: Original Student Tutorial
Practice plotting coordinates, in Quadrant I, using ordered pairs in this interactive tutorial for students.
Type: Original Student Tutorial
Learn about the basics of the coordinate plane by focusing on Quadrant I and see why the coordinate plane is useful in everyday life in this interactive tutorial.
Type: Original Student Tutorial
Learn how the standard algorithm for multiplying numbers works and practice your skills in this interactive tutorial.
Type: Original Student Tutorial
Learn how to use repeat loops in this interactive tutorial. Repeat loops iterate though a list of instructions based on a desired number of times. Combined with variables, condition statements, if statements, and repeat loops we practice using order of operations to code.
This is part 1 of a 4-part series. Click below to check out the other tutorials in the series.
- Bee A Coder Part 1: Declare Variables
- Bee A Coder Part 2: Condition Statements
- Bee A Coder Part 3: If Statements
Type: Original Student Tutorial
Learn how to perform instructions using an if statement and explore relational operators (less than, greater than, equal and not equal to) and how they are used to compare to values in this interactive tutorial.
Type: Original Student Tutorial
Construct efficient lines of code using condition- and if-statements to solve equations as you complete this interactive tutorial. You'll also review the order of operations in expressions.
This is part 2 of a 4-part series on coding. Click below to open the other tutorials in the series.
- Bee A Coder Part 1: Declare Variables
- Bee A Coder Part 3: If Statements
- Bee A Coder Part 4: Repeat Loops
Type: Original Student Tutorial
Learn how to define, declare and initialize variables as you start the journey to "bee" a coder in this interactive tutorial. Variables are structures used by computer programs to store information. You'll use your math skills to represent a fraction as a decimal to be stored in a variable.
This is part 1 of a 4-part series on coding. Click below to open the other tutorials in the series.
- Bee A Coder Part 2: Condition Statements
- Bee A Coder Part 3: If Statements
- Bee A Coder Part 4: Repeat Loops
Type: Original Student Tutorial
Learn how to write mathematical expressions while making faces in this interactive tutorial!
Type: Original Student Tutorial
Learn to interpret data presented on a line plot and use operations on fractions to solve problems involving information presented in line plots as you complete this beach-themed, interactive tutorial.
Type: Original Student Tutorial
Learn how to convert among different-sized customary units of weight, length, capacity, and units of time at the skate park in the this interactive tutorial.
Type: Original Student Tutorial
Learn to evaluate expressions that have all four operations (multiplication, division, addition, and subtraction) and parentheses as you settle debates in this interactive tutorial.
Type: Original Student Tutorial
By the end of this tutorial, you will be able to read and write decimals to the thousandths using base-ten numerals, number names, and expanded form.
Type: Original Student Tutorial
Learn to identify a fraction as division of the numerator by the denominator using fraction models in this interactive tutorial.
Type: Original Student Tutorial
Learn how to accurately plot coordinates on a plane in interactive tutorial.
Type: Original Student Tutorial
Demonstrate how a rectangular prism can be carefully filled without gaps or overlaps using the same size unit cubes and then use this model to determine its volume, in this interactive tutorial.
Type: Original Student Tutorial
Educational Games
This fun and interactive game helps practice estimation skills, using various operations of choice, including addition, subtraction, multiplication, division, using decimals, fractions, and percents.
Various levels of difficulty make this game appropriate for multiple age and ability levels.
Addition/Subtraction: The addition and subtraction of whole numbers, the addition and subtraction of decimals.
Multiplication/Division: The multiplication and addition of whole numbers.
Percentages: Identify the percentage of a whole number.
Fractions: Multiply and divide a whole number by a fraction, as well as apply properties of operations.
Type: Educational Game
This is a fun and interactive game that helps students practice ordering rational numbers, including decimals, fractions, and percents. You are planting and harvesting flowers for cash. Allow the bee to pollinate, and you can multiply your crops and cash rewards!
Type: Educational Game
Test your fraction skills by answering questions on this site. This quiz asks you to simplify fractions, convert fractions to decimals and percentages, and answer algebra questions involving fractions. You can even choose difficulty level, question types, and time limit.
Type: Educational Game
In this activity, students play a game of connect four, but to place a piece on the board they have to correctly estimate an addition, multiplication, or percentage problem. Students can adjust the difficulty of the problems as well as how close the estimate has to be to the actual result. This activity allows students to practice estimating addition, multiplication, and percentages of large numbers (100s). This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Educational Game
In this activity, students are quizzed on their ability to estimate sums, products, and percentages. The student can adjust the difficulty of the problems and how close they have to be to the actual answer. This activity allows students to practice estimating addition, multiplication, or percentages of large numbers. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Educational Game
This interactive applet gives students practice in making change in U.S. dollars and in four other currencies. Students are presented with a purchase amount and the amount paid, and they must enter the quantity of each denomination that make up the correct change. Students are rewarded for correct answers and are shown the correct change if they err. There are four levels of difficulty, ranging from amounts less than a dollar to amounts over $100.
Type: Educational Game
In this activity, students enter coordinates to make a path to get to a target destination while avoiding mines. This activity allows students to explore Cartesian coordinates and the Cartesian coordinate plane. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Educational Game
Educational Software / Tool
In this activity, students solve arithmetic problems involving whole numbers, integers, addition, subtraction, multiplication, and division. This activity allows students to track their progress in learning how to perform arithmetic on whole numbers and integers. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Educational Software / Tool
Problem-Solving Tasks
Students are asked to determine the number of unit cubes needed to construct cubes with given dimensions.
Type: Problem-Solving Task
Students are asked to find the volume of water in a tank that is 3/4 of the way full.
Type: Problem-Solving Task
Students are asked to find the height of a rectangular prism when given the length, width and volume.
Type: Problem-Solving Task
Students are asked to apply knowledge of volume of rectangular prisms to find the volume of an irregularly shaped object using the principle of displacement.
Type: Problem-Solving Task
The focus of this task is on understanding that fractions, in an explicit context, are fractions of a specific whole. In this this problem there are three different wholes: the medium pizza, the large pizza, and the two pizzas taken together. This task is best suited for instruction. Students can practice explaining their reasoning to each other in pairs or as part of a whole group discussion.
Type: Problem-Solving Task
The purpose of this task is to help develop students' understanding of addition of fractions; it is intended as an instructional task. Notice that students are not asked to find the sum so this may be given to students who are limited to computing sums of fractions with the same denominator. Rather, they need to apply a firm understanding of unit fractions (fractions with one in the numerator) and reason about their relative size.
Type: Problem-Solving Task
The purpose of this task is for students to solve multi-step problems in a context involving a concept that supports financial literacy, namely inflation. Inflation is a sustained increase in the average price level. In this task, students can see that if the price level increases and people’s incomes do not increase, they aren’t able to purchase as many goods and services; in other words, their purchasing power decreases.
Type: Problem-Solving Task
This task asks students to exercise both of these complementary skills, writing an expression in part (a) and interpreting a given expression in (b). The numbers given in the problem are deliberately large and "ugly" to discourage students from calculating Eric's and Leila's scores. The focus of this problem is not on numerical answers, but instead on building and interpreting expressions that could be entered in a calculator or communicated to another student unfamiliar with the context.
Type: Problem-Solving Task
This purpose of this task is to help students understand what happens when you scale the dimensions of a right rectangular solid. This task provides an opportunity to compare the relative volumes of boxes in order to calculate the mass of clay required to fill them. These relative volumes can be calculated geometrically, filling the larger box with smaller boxes, or arithmetically using the given dimensions.
Type: Problem-Solving Task
When a division problem involving whole numbers does not result in a whole number quotient, it is important for students to be able to decide whether the context requires the result to be reported as a whole number with remainder (as with Part (b)) or a mixed number/decimal (as with Part (c)). Part (a) presents two variations on a context that require these two different responses to highlight the distinction between them.
Type: Problem-Solving Task
The purpose of this task is to help students see the connection between a÷b and a/b in a particular concrete example. This task is probably best suited for instruction or formative assessment.
Type: Problem-Solving Task
This task provides a context for performing division of a whole number by a unit fraction. This problem is a "How many groups?'' example of division: the "groups'' in this case are the servings of oatmeal and the question is asking how many servings (or groups) there are in the package.
Type: Problem-Solving Task
The purpose of this task is to provide students with a situation in which it is natural for them to divide a unit fraction by a non-zero whole number. Determining the amount of paint that Kulani needs for each wall illustrates an understanding of the meaning of dividing a unit fraction by a non-zero whole number.
Type: Problem-Solving Task
The purpose of this task is for students to find the answer to a question in context that can be represented by fraction multiplication. This task is appropriate for either instruction or assessment depending on how it is used and where students are in their understanding of fraction multiplication.
Type: Problem-Solving Task
The purpose of this task is to present students with a situation in which they need to divide a whole number by a unit fraction in order to find a solution. Calculating the number of origami stars that Avery and Megan can make illustrates student understanding of the process of dividing a whole number by a unit fraction.
Type: Problem-Solving Task
The purpose of this task is to help students realize there are different ways to add mixed numbers and is most appropriate for use in an instructional setting. The two primary ways one can expect students to add are converting the mixed numbers to fractions greater than 1 or adding the whole numbers and fractional parts separately. It is good for students to develop a sense of which approach would be better in a particular context.
Type: Problem-Solving Task
The purpose of this instructional task is to motivate a discussion about adding fractions and the meaning of the common denominator. The different parts of the task have students moving back and forth between the abstract representation of the fractions and the meaning of the fractions in the context.
Type: Problem-Solving Task
This tasks lends itself very well to multiple solution methods. Students may learn a lot by comparing different methods. Students who are already comfortable with fraction multiplication can go straight to the numeric solutions given below. Students who are still unsure of the meanings of these operations can draw pictures or diagrams.
Type: Problem-Solving Task
The purpose of this task is to present students with a situation where it is natural to add fractions with unlike denominators; it can be used for either assessment or instructional purposes. Teachers should anticipate two types of solutions: one where students calculate the distance Alex ran to determine an answer, and one where students compare the two parts of his run to benchmark fractions.
Type: Problem-Solving Task
The purpose of this task is to familiarize students with multiplying fractions with real-world questions.
Type: Problem-Solving Task
The purpose of this task is to help students see that 4×(9+2) is four times as big as (9+2). Though this task may seem very simple, it provides students and teachers with a very useful visual for interpreting an expression without evaluating it because they can see for themselves that 4×(9+2) is four times as big as (9+2).
Type: Problem-Solving Task
The purpose of this task is to have students add fractions with unlike denominators and divide a unit fraction by a whole number. This accessible real-life context provides students with an opportunity to apply their understanding of addition as joining two separate quantities.
Type: Problem-Solving Task
The task could be one of the first activities for introducing the multiplication of fractions. The task has fractions which are easy to draw and provides a linear situation. Students benefit from reasoning through the solution to such word problems before they are told that they can be solved by multiplying the fractions; this helps them develop meaning for fraction multiplication.
Type: Problem-Solving Task
The solution uses the idea that multiplying by a fraction less than 1 results in a smaller value. The students need to explain why that is so.
Type: Problem-Solving Task
This is a good task to work with kids to try to explain their thinking clearly and precisely, although teachers should be willing to work with many different ways of explaining the relationship between the magnitude of the factors and the magnitude of the product.
Type: Problem-Solving Task
The purpose of this task is to generate a classroom discussion that helps students synthesize what they have learned about multiplication in previous grades. It builds on applying properties of operations as strategies to multiply and divide and interpreting a multiplication equation as a comparison.
Type: Problem-Solving Task
This problem allows student to see words that can describe an expression although the solution requires nested parentheses. Additionally , the words (add, sum) and (product, multiply) are all strategically used so that the student can see that these words have related meanings.
Type: Problem-Solving Task
This problem asks the student to evaluate six numerical expressions that contain the same integers and operations yet have differing results due to placement of parentheses. This type of problem helps students to see structure in numerical expressions. In later grades they will be working with similar ideas in the context of seeing and using structure in algebraic expressions.
Type: Problem-Solving Task
This task requires division of multi-digit numbers in the context of changing units. In addition, the conversion problem requires two steps since 2011 minutes needs to be converted first to hours and minutes and then to days, hours, and minutes.
Type: Problem-Solving Task
This is the third problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. The first, Running to school, does not require that the unit fractions that comprise 3/4 be subdivided in order to find 1/3 of 3/4. The second task, Drinking Juice, does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2. This task also requires subdivision and involves multiplying a fraction and a mixed number.
Type: Problem-Solving Task
The purpose of this task is to gain a better understanding of multiplying with fractions. Students should use the diagram provided to support their findings.
Type: Problem-Solving Task
This problem helps students gain a better understanding of multiplying with fractions.
Type: Problem-Solving Task
The purpose of this task is to provide students with a concrete experience they can relate to fraction multiplication. Perhaps more importantly, the task also purposefully relates length and locations of points on a number line, a common trouble spot for students. This task is meant for instruction and would be a useful as part of an introductory unit on fraction multiplication.
Type: Problem-Solving Task
Part (a) of this task asks students to use two different denominators to subtract fractions. The purpose of this is to help students realize that any common denominator will work, not just the least common denominator. Part (b) does not ask students to do it in more than one way; the purpose is to give them an opportunity to choose a denominator and possibly compare with another student who chose a different denominator. The purpose of part (c) is to help students move away from a reliance on drawing pictures. Students can draw a picture if they want, but this subtraction problem is easier to do symbolically, which helps students appreciate the power of symbolic notation.
Type: Problem-Solving Task
Part (a) of this task asks students to find and use two different common denominators to add the given fractions. The purpose of this question is to help students realize that they can use any common denominator to find a solution, not just the least common denominator. Part (b) does not ask students to solve the given addition problem in more than one way. Instead, the purpose of this question is to give students an opportunity to choose a denominator and possibly to compare their solution method with another student who chose a different denominator. The purpose of part (c) is to give students who are ready to work symbolically a chance to work more efficiently.
Type: Problem-Solving Task
The purpose of this task is to help students gain a better understanding of fractions and the conversion of fractions into smaller units.
Type: Problem-Solving Task
This task is intended to complement "How many servings of oatmeal?" and "Molly's run.'' All three tasks address the division problem 4÷1/3 but from different points of view. This task provides a how many in each group version of 4÷1/3. This task should be done together with the "How many servings of oatmeal" task with specific attention paid to the very different pictures representing the two situations.
Type: Problem-Solving Task
One goal of this task is to help students develop comfort and ease with adding fractions with unlike denominators. Another goal is to help them develop fraction number sense by having students decompose fractions.
Type: Problem-Solving Task
This is the second problem in a series of three tasks involving fraction multiplication that can be solved with pictures or number lines. This task does require students to subdivide the unit fractions that comprise 1/2 in order to find 3/4 of 1/2.
Type: Problem-Solving Task
This task addresses common errors that students make when interpreting adding fractions word problems. It is very important for students to recognize that they only add fractions when the fractions refer to the same whole, and also when the fractions of the whole being added do not overlap. This set of questions is designed to enhance a student's understanding of when it is and is not appropriate to add fractions.
Type: Problem-Solving Task
This task requires students to recognize both "number of groups unknown" (part (a)) and "group size unknown" (part (d)) division problems in the context of a whole number divided by a unit fraction. It also addresses a common misconception that students have where they confuse dividing by 2 or multiplying by 1/2 with dividing by 1/2.
Type: Problem-Solving Task
The purpose of this task is to have students think about the meaning of multiplying a number by a fraction, and use this burgeoning understanding of fraction multiplication to make sense of the commutative property of multiplication in the case of fractions.
Type: Problem-Solving Task
The purpose of this task is for students to compare a number and its product with other numbers that are greater than and less than one. As written, this task could be used in a summative assessment context, but it might be more useful in an instructional setting where students are asked to explain their answers either to a partner or in a whole class discussion.
Type: Problem-Solving Task
This particular problem deals with multiplication. Even though students can solve this problem by multiplying, it is unlikely they will. Here it is much easier to answer the question if you can think of multiplying a number by a factor as scaling the number.
Type: Problem-Solving Task
The purpose of this task is to provide students with a concrete situation they can model by dividing a whole number by a unit fraction. For students who are just beginning to think about the meaning of division by a unit fraction (or students who have never cooked), the teacher can bring in a 1/4 cup measuring cup so that students can act it out. If students can reason through parts (a) and (b) successfully, they will be well-situated to think about part (c) which could yield different solution methods.
Type: Problem-Solving Task
Tutorials
This Khan Academy tutorial video explains patterns in the placement of the decimal point, when a decimal is multiplied by a power of 10. Exponents are NOT discussed.
Type: Tutorial
This Khan Academy tutorial video presents the methodology of understanding and using patterns in the number of zeros of products that have a factor that is a power of 10. While the standard does not mention exponents, the place value understanding of multiplying or dividing by powers of ten will help students understand multiplying and dividing by decimals.
Type: Tutorial
This Khan Academy tutorial video presents the pattern, when multiplying tens, that develops when we compare the number of factors of tens with the number of zeros in the product. The vocabulary, exponent and base, are introduced.
Type: Tutorial
This Khan Academy tutorial video interprets written statements and writes them as mathematical expressions.
Type: Tutorial
This Khan Academy tutorial video presents the impact of parentheses notation in an expression. As the tutorial does the same problem with and without parenthesis, negative numbers are part of the solution.
Type: Tutorial
This Khan Academy tutorial video demonstrates how to write a simple expression from a word problem.
Type: Tutorial
This Khan Academy tutorial video illustrates the conversion equivalence of liters, milliliters, and kiloliters.
Type: Tutorial
This Khan Academy tutorial video presentation represents a word problem's solution on a coordinate plane to determine the number of blocks walked from a home to a school.
Type: Tutorial
This Khan Academy tutorial video presents how to graph an ordered pair of positive numbers on the x- and y-axis of a coordinate plane.
Type: Tutorial
This Khan Academy tutorial video presents a strategy for solving the following problem: given a dot plot with different measurements of trail mix in bags, find the amount of trail mix each bag would contain, if the total amount in all the bags was equally redistributed.
Type: Tutorial
This Khan Academy tutorial video develops a visual diagram to use to solve a distance problem that requires converting feet to yards and other computations.
Type: Tutorial
This Khan Academy tutorial video demonstrates a strategy for ordering four different-sized metric length units.
Type: Tutorial
This Khan Academy tutorial video illustrates how to find the volume of an irregular solid figure by dividing the figure into two rectangular prisms and finding the volume of each. Although the tutorial works from a drawing, individual volume cubes are not drawn so students must work from the formula.
Type: Tutorial
This Khan Academy tutorial video illustrates finding the volume of an irregular figure made up of unit cubes by separating the figure into two rectangular prisms and finding the volume of each part.
Type: Tutorial
This Khan Academy tutorial video illustrates measuring volume by counting unit cubes. Models in this video include composite figure of rectangular prisms although only counting is used to find volume, not an equation.
Type: Tutorial
This Khan Academy tutorial video describes measurement in one, two, and three dimensions.
Type: Tutorial
This Khan Academy tutorial video introduces quadrilaterals. their categories, and subcategories.
Type: Tutorial
In this Khan Academy tutorial video two decimals are compared using grid diagrams.
Type: Tutorial
This Khan Academy tutorial video presents using place-value to compare two decimals expressed to thousandths.
Type: Tutorial
In this video, you will work through an example to correctly use the order of operations.
Type: Tutorial
In this video, you will see why it is important to have one agreed upon order of operations.
Type: Tutorial
In this video tutorial from Khan Academy, learn about the importance of place value when dividing. The tutorial uses place value up to thousands to help students think about division.
Type: Tutorial
In this video tutorial from Khan Academy, view a demonstration of how to set-up an area model for multiplying a two-digit number by a two-digit number on graph or grid paper and then link this to the standard algorithm.
Type: Tutorial
In this tutorial video from Khan Academy, view an example of how to multiply a two-digit number by a two-digit number using the area model. The video makes a connection between partial products and the area model.
Type: Tutorial
In this video tutorial from Khan Academy, view an example and a description of how the distributive property can be used to multiply a two-digit number by a two-digit number. The second example uses the area model with the distributive property.
Type: Tutorial
In this Khan Academy video tutorial, view an example of multiplying a 4-digit number by a 1-digit number by expanding the 4-digit number and multiplying by each digit individually in an area model. This video will help to build an understanding before teaching the standard algorithm. Multiplying with a 4-digit factor is larger than some standards which limit factors to 3-digits.
Type: Tutorial
In this tutorial video from Khan Academy, view an example of how to multiply a 2-digit number by another 2-digit number. Be sure to stick around for the second example! The key is understanding the value of each digit!
Type: Tutorial
In this video tutorial from Khan Academy, view an example of how to solve a problem in which a 3-digit number is being multiplied by a 1-digit number using the standard algorithm.
Type: Tutorial
In this video tutorial from Khan Academy, view an example of how to solve a multiplication problem with a two-digit number multiplied by a one-digit number using the standard algorithm.
Type: Tutorial
In this tutorial, the four operations are applied to fractions with the visualization of the number line. This tutorial starts by adding fractions with the same denominators and explains the logic behind multiplication of fractions. This tutorial also highlights the application and extension of previous understandings of mulitplication to multiply a fraction or whole number by a fraction.
a. Interpret the product (a/b) x q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a x q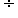 b. In general, (a/b) x (c/d) = ac/bd.
b. In general, (a/b) x (c/d) = ac/bd.
Type: Tutorial
This tutorial explores the addition and subtraction of fractions with unlike denominators. Using the number line, this mathematical process can be easily visualized and connected to the final strategy of multiplying the denominators (a/b + c/d = ad +bc/bd). The video number line does show negative numbers which goes beyond elementary standards so an elementary teacher would need to reflect on whether this video will enrich student knowledge or cause confusion.
Type: Tutorial
In this tutorial, students will be exposed to the strategy of finding the least common denominator for certain cases. Elementary teachers should note this is not a requirement for elementary standards and consider whether this video will further student knowledge or create confusion. This chapter explains how to find the smallest possible common denominator. For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12.
Type: Tutorial
The Cartesian Coordinate system, formed from the Cartesian product of the real number line with itself, allows algebraic equations to be visualized as geometric shapes in two or three dimensions. While this tutorial includes the basis of Coordinate system, it also includes ideas beyond fifth grade standards. Most likely only advanced fifth graders would find the video engaging.
Type: Tutorial
This tutorial for student audiences will assist learners with a further understanding of the rules for adding and subtracting with decimals. Students will be able to navigate the teaching portion of the tutorial at their own pace and test their understanding after each step of the lesson with a "Try This" section. The "Try This" section will monitor students answers and self-check by a right answer turning orange and a wrong answer dissolving.
Type: Tutorial
This tutorial for student audiences will assist learners with a further understanding of the rules for adding and subtracting fractions. Students will be able to navigate the teaching portion of the tutorial at their own pace and test their understanding after each step of the lesson with a "Try This" section. The "Try This" section will monitor students answers and self-check by a right answer turning orange and a wrong answer dissolving.
Type: Tutorial
In this lesson, students will be viewing a Khan Academy video that will show how to convert ratios using speed units.
Type: Tutorial
The video describes how to multiply fractions and state the answer in lowest terms.
Type: Tutorial
Virtual Manipulatives
This virtual manipulative allows individual students to work with fraction relationships. (There is also a link to a two-player version.)
Type: Virtual Manipulative
In this activity, students practice solving algebraic expressions using order of operations. The applet records their score so the student can track their progress. This activity allows students to practice applying the order of operations when solving problems. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the java applet.
Type: Virtual Manipulative


 Create CMAP
Create CMAP





