MA.912.AR.1.1
Examples
Algebra 1 Example: Derrick is using the formula 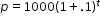 to make a prediction about the camel population in Australia. He identifies the growth factor as (1+.1), or 1.1, and states that the camel population will grow at an annual rate of 10% per year.
to make a prediction about the camel population in Australia. He identifies the growth factor as (1+.1), or 1.1, and states that the camel population will grow at an annual rate of 10% per year.
Example: The expression 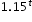 can be rewritten as
can be rewritten as 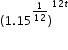 which is approximately equivalent to
which is approximately equivalent to 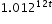 . This latter expression reveals the approximate equivalent monthly interest rate of 1.2% if the annual rate is 15%.
. This latter expression reveals the approximate equivalent monthly interest rate of 1.2% if the annual rate is 15%.
Clarifications
Clarification 1: Parts of an expression include factors, terms, constants, coefficients and variables.
Clarification 2: Within the Mathematics for Data and Financial Literacy course, problem types focus on money and business.
Alternate version of this benchmark for students with significant cognitive disabilities.
Connecting Benchmarks/Horizontal Alignment
- MA.912.NSO.1.2
- MA.912.AR.2.2
- MA.912.AR.2.5
- MA.912.AR.2.6
- MA.912.AR.3.1
- MA.912.AR.3.6
- MA.912.AR.3.7
- MA.912.AR.3.8
- MA.912.AR.4.1
- MA.912.AR.5.3
- MA.912.AR.5.6
- MA.912.FL.3.2
Terms from the K-12 Glossary
- Coefficient
- Expression
- Equation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students generated and identified equivalent linear expressions, and solved multi-step problems involving linear expressions within real-world contexts. In Algebra I, students generate and interpret equivalent linear, absolute value, quadratic and exponential expressions and equations. In later courses, students will identify and interpret other functional (exponential, rational, logarithmic, trigonometric, etc.) expressions and equations.- Instruction includes making the connection to linear, absolute value, quadratic and
exponential functions.
- Students should be able to identify factors, terms, constants, coefficients and
variables in expressions and equations.
- Go beyond these popular parts of an expression and equation: the growth/decay factor in exponential functions, rate of change in linear functions, interest, etc.
- Look for opportunities to interpret these components in context – make these discussions part of daily instruction.
- Students should be able to identify factors, terms, constants, coefficients and
variables in expressions and equations.
Common Misconceptions or Errors
- Students may not be able to identify parts of an expression and equation or interpret those
parts within context. Ensure these are embedded throughout instruction and discussions.
- For example, building in questions to identify these parts and discussing their connection to the context in which they represent in a routine way will help students to make these connections.
Strategies to Support Tiered Instruction
- Teacher facilitates discussions which include questions and clarifications to identify the connections of expressions and equations to the context of problems.
- Instruction provides opportunities to increase understanding of vocabulary terms.
- For example, instruction may include a vocabulary review using a chart shown.
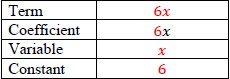
- For example, instruction may include a vocabulary review using a chart shown.
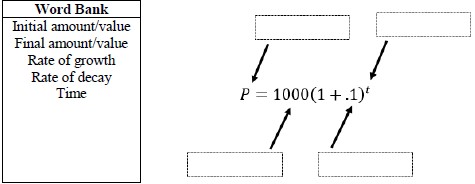
- Teacher provides students with an expression or equation and allows them to match the parts to key vocabulary.
- For example, teacher can provide the word bank to identify the different parts of
the equation shown.
Instructional Tasks
Instructional Task 1 (MTR.5.1)- The algebraic expression ( − 1)2 + (2 − 1) can be used to calculate the number of symbols in each diagram below. Explain what likely represents, how the parts of this expression relate to the diagrams, and why the expression results in the number of symbols in each diagram.

- Last weekend, Cindy purchased two tops, a pair of pants, and a skirt at her favorite store. The
equation = 1.075 can be used to calculate her total cost where represents the pretax
subtotal cost of her purchase.
- Part A. In the equation = 1.075, what does the number 1 represent? Explain using the context of Cindy’s situation.
- Part B. In the equation = 1.075, what does the number 0.075 represent? Explain using the context of Cindy’s situation.
Instructional Items
Instructional Item 1- Identify the factors in the expression 2(3 − 1) + 2(2 + 2).
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Algebraic Reasoning
Standard: Interpret and rewrite algebraic expressions and equations in equivalent forms.
Date Adopted or Revised: 08/20
Status: State Board Approved
This benchmark is part of these courses.
