Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.★
- Factor a quadratic expression to reveal the zeros of the function it defines.
- Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.
- Use the properties of exponents to transform expressions for exponential functions. For example the expression
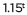 can be rewritten as
can be rewritten as 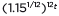 ≈
≈ 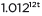 to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
-
Also assesses:
- Assessment Limits :
Items that require the student to transform a quadratic equation to
vertex form, b/a must be an even integer.For A-SSE.1.1, items should not ask the student to interpret zeros, the
vertex, or axis of symmetry when the quadratic expression is in the
form ax² + bx + c (see F-IF.3.8).For A-SSE.2.3c and A-SSE.1.1, exponential expressions are limited to
simple growth and decay. If the number e is used then its
approximate value should be given in the stem.For A-SSE.2.3a and A-SSE.1.1, quadratic expressions should be
univariate.For A-SSE.2.3b, items should only ask the student to interpret the yvalue of the vertex within a real-world context.
For A-SSE.2.3, items should require the student to choose how to
rewrite the expression.In items that require the student to write equivalent expressions by
factoring, the given expression may- have integral common factors
- be a difference of two squares up to a degree of 4
- be a quadratic, ax² + bx + c, where a > 0 and a, b, and c are integers
- be a polynomial of four terms with a leading coefficient of 1 and highest degree of 3.
- Calculator :
Neutral
- Clarification :
Students will use equivalent forms of a quadratic expression to
interpret the expression’s terms, factors, zeros, maximum, minimum,
coefficients, or parts in terms of the real-world situation the
expression represents.
Students will use equivalent forms of an exponential expression to
interpret the expression’s terms, factors, coefficients, or parts in
terms of the real-world situation the expression represents.Students will rewrite algebraic expressions in different equivalent
forms by recognizing the expression’s structure.Students will rewrite algebraic expressions in different equivalent
forms using factoring techniques (e.g., common factors, grouping, the
difference of two squares, the sum or difference of two cubes, or a
combination of methods to factor completely) or simplifying
expressions (e.g., combining like terms, using the distributive
property, and other operations with polynomials). - Stimulus Attributes :
Items assessing A-SSE.2.3 and A-SSE.1.1 must be set in a real-world
context.Items that require an equivalent expression found by factoring may
be in a real-world or mathematical context.Items should contain expressions only.
Items may require the student to provide the answer in a specific
form. - Response Attributes :
Items may require the student to choose an appropriate level of
accuracy.Items may require the student to choose and interpret units.
For A-SSE.1.1 and A-SSE.2.3, items may require the student to apply
the basic modeling cycle.
MAFS.912.A-SSEE.1.1
MAFS.912.A-SSE.1.2
- Test Item #: Sample Item 1
- Question:
Sue removes the plug from a trough to drain the water inside. The volume, in gallons, in the trough after it has been unplugged can be modeled by 4t²-32t+63, where t is time, in minutes.
A. Click on the correct property that will give Sue the amount of time it takes the trough to drain.
B. Click on the expression that will reveal the property.
- Difficulty: N/A
- Type: SHT: Selectable Hot Text
Related Courses
Related Access Points
Related Resources
Formative Assessments
Lesson Plans
Original Student Tutorials
Problem-Solving Tasks
Tutorial
Unit/Lesson Sequence
MFAS Formative Assessments
Students are asked to transform an exponential expression so that the rate of change corresponds to a different time interval.
Students are asked to find the zeros of a quadratic function in the context of a modeling problem.
Students are asked to use the properties of exponents to show that two expressions are equivalent and compare the two functions in terms of what each reveals.
Students are asked to rewrite a quadratic expression in vertex form to find maximum and minimum values.
Original Student Tutorials Mathematics - Grades 9-12
Learn to complete the square of a quadratic expression and identify the maximum or minimum value of the quadratic function it defines. In this interactive tutorial, you'll also interpret the meaning of the maximum and minimum of a quadratic function in a real world context.
Learn to find the zeros of a quadratic function and interpret their meaning in real-world contexts with this interactive tutorial.
Learn the process of completing the square of a quadratic function to find the maximum or minimum to discover how high a dolphin jumped in this interactive tutorial.
This is part 1 of a 2 part series. Click HERE to open Part 2.
Learn the process of completing the square of a quadratic function to find the maximum or minimum to discover how high a dolphin jumped in this interactive tutorial.
This is part 2 of a 2 part series. Click HERE to open part 1.
Student Resources
Original Student Tutorials
Learn the process of completing the square of a quadratic function to find the maximum or minimum to discover how high a dolphin jumped in this interactive tutorial.
This is part 2 of a 2 part series. Click HERE to open part 1.
Type: Original Student Tutorial
Learn the process of completing the square of a quadratic function to find the maximum or minimum to discover how high a dolphin jumped in this interactive tutorial.
This is part 1 of a 2 part series. Click HERE to open Part 2.
Type: Original Student Tutorial
Learn to find the zeros of a quadratic function and interpret their meaning in real-world contexts with this interactive tutorial.
Type: Original Student Tutorial
Learn to complete the square of a quadratic expression and identify the maximum or minimum value of the quadratic function it defines. In this interactive tutorial, you'll also interpret the meaning of the maximum and minimum of a quadratic function in a real world context.
Type: Original Student Tutorial
Problem-Solving Tasks
There are many different ways to write exponential expressions that describe the same quantity, in this task the amount of a radioactive substance after t years. Depending on what aspect of the context we need to investigate, one expression of the quantity may be more useful than another. This task contrasts the usefulness of four equivalent expressions. Students first have to confirm that the given expressions for the radioactive substance are equivalent. Then they have to explain the significance of each expression in the context of the situation.
Type: Problem-Solving Task
In this resource, a method of deriving the quadratic formula from a theoretical standpoint is demonstrated. This task is for instructional purposes only and builds on "Building an explicit quadratic function."
Type: Problem-Solving Task
This task compares the usefulness of different forms of a quadratic expression. Students have to choose which form most easily provides information about the maximum value, the zeros and the vertical intercept of a quadratic expression in the context of a real world situation. Rather than just manipulating one form into the other, students can make sense out of the structure of the expressions.
(From Algebra: Form and Function, McCallum et al., Wiley 2010)
Type: Problem-Solving Task
The purpose of this task is to help students see manipulation of expressions as an activity undertaken for a purpose.
Variation 1 of this task presents a related more complex expression already in the correct form to answer the question.
The expression arises in physics as the reciprocal of the combined resistance of two resistors in parallel. However, the context is not explicitly considered here.
Type: Problem-Solving Task
This task illustrates the process of rearranging the terms of an expression to reveal different aspects about the quantity it represents, precisely the language being used in standard MAFS.912.A-SSE.2.3. Students are provided with an expression giving the temperature of a container at a time t, and have to use simple inequalities (e.g., that 2t>0 for all t) to reduce the complexity of an expression to a form where bounds on the temperature of a container of ice cream are made apparent.
Type: Problem-Solving Task
Students compare graphs of different quadratic functions, then produce equations of their own to satisfy given conditions.
This exploration can be done in class near the beginning of a unit on graphing parabolas. Students need to be familiar with intercepts, and need to know what the vertex is. It is effective after students have graphed parabolas in vertex form (y=a(x–h)2+k), but have not yet explored graphing other forms.
Type: Problem-Solving Task
The purpose of this task is to identify the structure in the two algebraic expressions by interpreting them in terms of a geometric context. Students will have likely seen this type of process before, so the principal source of challenge in this task is to encourage a multitude and variety of approaches, both in terms of the geometric argument and in terms of the algebraic manipulation.
Type: Problem-Solving Task
Tutorial
This tutorial demonstrates how to use the power of a power property with both numerals and variables.
Type: Tutorial
Parent Resources
Problem-Solving Tasks
There are many different ways to write exponential expressions that describe the same quantity, in this task the amount of a radioactive substance after t years. Depending on what aspect of the context we need to investigate, one expression of the quantity may be more useful than another. This task contrasts the usefulness of four equivalent expressions. Students first have to confirm that the given expressions for the radioactive substance are equivalent. Then they have to explain the significance of each expression in the context of the situation.
Type: Problem-Solving Task
In this resource, a method of deriving the quadratic formula from a theoretical standpoint is demonstrated. This task is for instructional purposes only and builds on "Building an explicit quadratic function."
Type: Problem-Solving Task
This task compares the usefulness of different forms of a quadratic expression. Students have to choose which form most easily provides information about the maximum value, the zeros and the vertical intercept of a quadratic expression in the context of a real world situation. Rather than just manipulating one form into the other, students can make sense out of the structure of the expressions.
(From Algebra: Form and Function, McCallum et al., Wiley 2010)
Type: Problem-Solving Task
The purpose of this task is to help students see manipulation of expressions as an activity undertaken for a purpose.
Variation 1 of this task presents a related more complex expression already in the correct form to answer the question.
The expression arises in physics as the reciprocal of the combined resistance of two resistors in parallel. However, the context is not explicitly considered here.
Type: Problem-Solving Task
This task illustrates the process of rearranging the terms of an expression to reveal different aspects about the quantity it represents, precisely the language being used in standard MAFS.912.A-SSE.2.3. Students are provided with an expression giving the temperature of a container at a time t, and have to use simple inequalities (e.g., that 2t>0 for all t) to reduce the complexity of an expression to a form where bounds on the temperature of a container of ice cream are made apparent.
Type: Problem-Solving Task
Students compare graphs of different quadratic functions, then produce equations of their own to satisfy given conditions.
This exploration can be done in class near the beginning of a unit on graphing parabolas. Students need to be familiar with intercepts, and need to know what the vertex is. It is effective after students have graphed parabolas in vertex form (y=a(x–h)2+k), but have not yet explored graphing other forms.
Type: Problem-Solving Task
The purpose of this task is to identify the structure in the two algebraic expressions by interpreting them in terms of a geometric context. Students will have likely seen this type of process before, so the principal source of challenge in this task is to encourage a multitude and variety of approaches, both in terms of the geometric argument and in terms of the algebraic manipulation.
Type: Problem-Solving Task
Tutorial
This tutorial demonstrates how to use the power of a power property with both numerals and variables.
Type: Tutorial