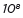Word (.docx)
Acrobat (.pdf)
and the population
of the world as 7 ×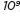 
, and determine that the world population is more
than 20 times larger.
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
- Assessment Limits :
N/A
- Calculator :
No
- Context :
Allowable
- Test Item #: Sample Item 1
- Question:
The average mass of a giraffe is approximately
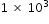kilograms. The average mass of a blue whale is approximately 
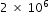.About how many times more mass does a blue whale have than a giraffe?
- Difficulty: N/A
- Type: EE: Equation Editor
- Test Item #: Sample Item 2
- Question:
The average mass of an ant is approximately
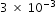grams. The average mass of a giraffe is approximately 
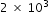kilograms.About how many times more mass does a giraffe have than an ant?
- Difficulty: N/A
- Type: EE: Equation Editor
Related Courses
Related Access Points
Related Resources
Formative Assessments
Students are asked to estimate an extremely large and an extremely small number by writing it in the form a x 
.
Type: Formative Assessment
Lesson Plan
Original Student Tutorial
Problem-Solving Tasks
Student Center Activity
MFAS Formative Assessments
Students are given pairs of numbers written in scientific notation and are asked to compare them multiplicatively.
Students are asked to estimate an extremely large and an extremely small number by writing it in the form a x 
.
Students are given pairs of numbers written in exponential form and are asked to compare them multiplicatively.
Students are given pairs of numbers written in the form of an integer times a power of 10 and are asked to compare the numbers in each pair using the inequality symbols.
Original Student Tutorials Mathematics - Grades 6-8
Explore how to express large quantities using scientific notation in this interactive tutorial.
Student Resources
Original Student Tutorial
Explore how to express large quantities using scientific notation in this interactive tutorial.
Type: Original Student Tutorial
Problem-Solving Task
The goal of this task is to give students a context to investigate large numbers and measurements. Students need to fluently convert units with very large numbers in order to successfully complete this task. The total number of pennies minted either in a single year or for the last century is phenomenally large and difficult to grasp. One way to assess how large this number is would be to consider how far all of these pennies would reach if we were able to stack them one on top of another: this is another phenomenally large number but just how large may well come as a surprise.
Type: Problem-Solving Task
Student Center Activity
Students can practice answering mathematics questions on a variety of topics. With an account, students can save their work and send it to their teacher when complete.
Type: Student Center Activity
Parent Resources
Problem-Solving Tasks
The goal of this task is to give students a context to investigate large numbers and measurements. Students need to fluently convert units with very large numbers in order to successfully complete this task. The total number of pennies minted either in a single year or for the last century is phenomenally large and difficult to grasp. One way to assess how large this number is would be to consider how far all of these pennies would reach if we were able to stack them one on top of another: this is another phenomenally large number but just how large may well come as a surprise.
Type: Problem-Solving Task
In this problem students are comparing a very small quantity with a very large quantity using the metric system. The metric system is especially convenient when comparing measurements using scientific notations since different units within the system are related by powers of ten.
Type: Problem-Solving Task
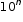