Use the formula 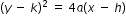 or formula
or formula 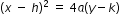 for a parabola to write the equation when given the focus and directrix.
for a parabola to write the equation when given the focus and directrix.
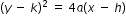 or formula
or formula 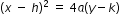 for a parabola to write the equation when given the focus and directrix.
for a parabola to write the equation when given the focus and directrix.
Clarifications:
Essential Understandings
Concrete:
- Identify objects that have the shape of a parabola, half an egg, satellite dish and the path the water is making out of the fountain.

- Throw an object in the air and draw a picture of the path the object takes. Click Here
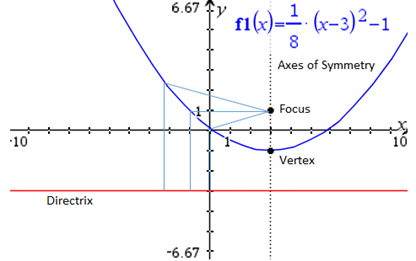
- Understand that a parabola is set of all points in a plane which are an equal distance away from a given point and given line (illustrated by the blue lines in the diagram below). The point is called the focus of the parabola, and the line is called the directrix.
- Understand that
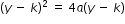 represents the vertical parabola and
represents the vertical parabola and 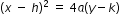 represents the horizontal parabola.
represents the horizontal parabola. - Identify what the variables represent in the formula.
- Understand that the vertex is the midpoint between the focus and the directrix that can be found using the formula y=k-a where y is the directrix, a is half the distance from the focus to the directrix and k is the y value of the vertex. For example: given a focus of (1,0) and a directrix y=-2, the distance between the focus and the directrix is 2. The distance from the focus to the vertex is 1. The directrix y=-2 is added to the distance from the directrix to the vertex, -2+1=-1. The y value of the vertex =-1. The x value of the vertex is the same as the focus x value, 1. The vertex of the parabola is (1,-1).
- Understand that given a graph a student can count the distance between the focus and the directrix. When this distance is divided in half it gives you the distance to the vertex, (a).
- Understand that the vertex is a point represented by an ordered pair (h,k). Understand that the x value from the vertex represents h and the y value from the vertex represents k.
- Understand that parabolas can open vertically and horizontally. Parabolas that open horizontally have a directrix with an x instead of a y. The formula for the directrix of a horizontal parabola is x=h-a. The y value of the vertex is identical to the y value of the focus.
- Substitute values into the equation for a parabola. For example: Given a parabola with a focus (1,0) and a directrix of y=-2. The distance between the vertex and the directrix = 1.
h = 1, k=-1 from the vertex (1,-1)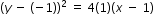
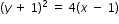
General Information
Number: MAFS.912.G-GPE.1.AP.2a
Category: Access Points
Date Adopted or Revised:
06/14
Cluster:
Translate between the geometric description and the equation for a conic section. (Geometry - Additional Cluster) (Algebra 2 - Additional Cluster) :
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Related Standards
This access point is an alternate version of the following benchmark(s).
Related Courses
This access point is part of these courses.
Related Resources
Vetted resources educators can use to teach the concepts and skills in this access point.
Student Resources
Vetted resources students can use to learn the concepts and skills in this access point.
Parent Resources
Vetted resources caregivers can use to help students learn the concepts and skills in this access point.