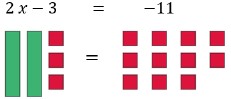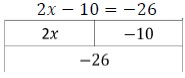Generated on 10/21/2025 at 4:05 PM
The webpage this document was printed/exported from can be found at the following URL:
https://www.cpalms.org/PreviewStandard/Preview/15463
Write and solve two-step equations in one variable within a mathematical or real-world context, where all terms are rational numbers.
Standard #: MA.7.AR.2.2
Standard Information
Standard Clarifications
Clarification 1: Instruction focuses the application of the properties of equality. Refer to Properties of Operations, Equality and Inequality (Appendix D).

Clarification 2: Instruction includes equations in the forms px±q=r and p(x±q)=r, where p, q and r are specific rational numbers.

Clarification 3: Problems include linear equations where the variable may be on either side of the equal sign.

General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 7
Strand: Algebraic Reasoning
Standard: Write and solve equations and inequalities in one variable.
Date Adopted or Revised: 08/20
Status: State Board Approved
Standard Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Equation
  • Rational Number

 

Vertical Alignment

Previous Benchmarks

Next Benchmarks

 

Purpose and Instructional Strategies

In grade 6, students are building on their ability to write and solve one-step equations with an emphasis on operations with linear expressions. In grade 7, students write and solve two-step equations. In grade 8, students solve multi-step linear equations (MTR.5.1). 
  • Instruction includes real-world contexts as well as linear equations where the variable may be on either side of the equal sign (MTR.7.1).
  • Instruction includes students verbalizing or writing the Properties of Operations and Properties of Equality (see Appendix D) used at each step to their solution.
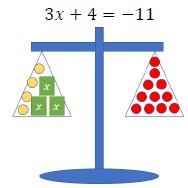
  • Use models or manipulatives, such as algebra tiles, bar diagrams or balances, to conceptualize equations (MTR.2.1).
    • Algebra Tiles
      2x-3=-11 on Algebra Tiles
    • Bar Diagrams
      2x-10=-26 on bar diagram
    • Balances
      3x+4=-11 on balances
  • Avoid a particular order when solving and allow students to proceed in multiple ways that are mathematically accurate.
    • For example, in the equation 4(x + 7) = 12, students may choose to divide both sides of the equation by 4 or use the Distributive Property with the 4. Compare the various strategies and ask students to determine which will be most efficient given different problem stems (MTR.3.1).

 

Common Misconceptions or Errors

  • Some students may incorrectly use the addition and subtraction properties of equality on the same side of the equal sign while solving an equation. To address this misconception, use manipulatives such as balances, algebra tiles or bar diagrams to show the balance between the two sides of an equation (MTR.2.1).
  • Students may incorrectly identify the constants and the coefficients within a real-world context of the problem.

 

Strategies to Support Tiered Instruction

  • Teacher provides opportunities for students to practice solving equations using the addition and subtraction properties of equality using an interactive computer equation balance, manipulatives and other visual representations.
  • Teacher provides support for students in identifying the coefficients and constants within a real-world context of the problem. Present students with examples of real-world problems that can be solved with equations.
    • For example, Cameron’s fish tank can hold 12 gallons of water and he adds 2.5 gallons of water a minute. If there are already 3.4 gallons of water in the tank, for how many minutes can Cameron fill his tank without overflowing?
  • Teacher provides opportunities for students to comprehend the context or situation by engaging in questions (laminating these questions on a printed card for students to utilize as a resource in and out of the classroom would be helpful).
    • What do you know from the problem?
    • What is the problem asking you to find?
    • Can you create a visual model to help you understand or see patterns in your problem?
  • Teacher provides opportunities for students to use algebra tiles to co-solve provided equations with the teacher without the need of writing the equation first.
  • Teacher provides opportunities for students to co-write an algebraic equation with the teacher without requiring students to solve the equation.
  • Instruction includes the use of a three-read strategy. Students read the problem three different times, each with a different purpose (laminating these questions on a printed card for students to utilize as a resource in and out of the classroom would be helpful).
    • First, read the problem with the purpose of answering the question: What is the problem, context, or story about?
    • Second, read the problem with the purpose of answering the question: What are we trying to find out?
    • Third, read the problem with the purpose of answering the question: What information is important in the problem?
  • Teacher models the use manipulatives such as balances, algebra tiles or bar diagrams to show the balance between the two sides of an equation.

 

Instructional Tasks

Instructional Task 1 (MTR.1.1, MTR.7.1)
A plumber has been called in to replace a broken kitchen sink. The material needed costs $341.25 and the total expected cost of the job is $424.09. How many hours will the plumber need to work in order to get the job completed?
  • Part A. What questions would need to be answered to approach this problem? Is there enough information given to solve the problem? Why or why not?
  • Part B. The average rate for a plumber in Florida is $20.71 per hour. Write and solve an equation to determine how many hours the plumber will be working.

Instructional Task 2 (MTR.5.1)
The length of the rectangle is twice its width. The perimeter of the rectangle totals 45 feet. What is the width of the rectangle?

 

Instructional Items

Instructional Item 1
What is the exact value of x in the equation 79 = 23x − 7?

Instructional Item 2
What is the value of z in the equation 5.6(z − 2) = 11?

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
Related Courses
Related Access Points
  • MA.7.AR.2.AP.2a # Set up two-step equations in one variable based on real-world problems.
  • MA.7.AR.2.AP.2b # Solve two-step equations in one variable based on real-world problems, where all terms have positive integer coefficients.
Related Resources
Educational Game
  • Algebra Four # In this activity, two students play a simulated game of Connect Four, but in order to place a piece on the board, they must correctly solve an algebraic equation. This activity allows students to practice solving equations of varying difficulty: one-step, two-step, or quadratic equations and using the distributive property if desired. This activity includes supplemental materials, including background information about the topics covered, a description of how to use the application, and exploration questions for use with the Java applet.
Formative Assessments
  • Solve Equations # Students are asked to solve two equations involving rational numbers.
  • Write and Solve an Equation # Students are asked to write and solve a two-step equation to model the relationship among variables in a given scenario.
  • Squares # Students are asked to write and solve an equation of the form p(x + q) = r in the context of a problem about the perimeter of a square.
  • Algebra or Arithmetic? # Students are asked to compare an arithmetic solution to an algebraic solution of a word problem.
Lesson Plans
  • A Florida Vacation # Students will calculate sales tax to plan a family vacation budget. Through collaborative learning activities and discussions, students will understand the concept of sales tax as a civic responsibility and recognize the importance of considering sales tax in their financial planning to contribute to their community’s public service and infrastructure in this integrated lesson plan.
  • How Will the Ninja Capture the Valuable Princess? # This lesson allows students to solve two-step equations involving a mythological story line in which the princess (variable) is protected by a bodyguard (number added or subtracted in an equation) and by a protector (number multiplied or divided by the variable). The three characters live in a castle, surrounded by the moat (equal sign) and an innocent bystander that lives outside the castle (number on the opposite side of the variable). However, Ninjas are infiltrating the castle to steal the “valuable” princess. Using this story line, students must then decide who the Ninja must eliminate first to get to the princess. This lesson can also be used to solve equations with like terms on the same side and equations with the same variable on each side.
  • Lost in Translation? Verbal and Algebraic Representations of Expressions and Equations # This lesson is designed to assist in teacher facilitation of student understanding related to the concept of translating between verbal and algebraic two-step equations. 
  • Solving Linear Equations # Students practice writing and solving two-step linear equations using the properties of equality and distributive property. They represent real-world and mathematical situations with equations in the forms px + q = r and p (x + q) = r.
  • Company Charges # In this lesson, students will learn how to write and solve linear equations that have one solution, infinitely many solutions, and no solutions. As the students decipher word problems, they will recognize which elements of equations affect the number of possible solutions. This lesson is guided by a PowerPoint presentation.
  • Pennies and Post-its # Students will use manipulatives (pennies and post-its) to model solving one-variable equations.
  • Inequal-tile-ies # In this lesson, students will work with Algebra Tiles to solve inequalities. This lesson builds upon student experience with solving equalities, as well as identifying inequalities and representing them on the number line. This lesson is an introduction to solving inequalities.
  • Relating Surface Area and Volume # Students will recognize that while the surface area may change, the volume can remain the same. This lesson is enhanced through the multimedia CPALMS Perspectives Video, which introduces students to the relationship between surface area and volume.
  • Solving Linear Equations in One Variable # This lesson unit is intended to help you assess how well students are able to:
    • Solve linear equations in one variable with rational number coefficients.
    • Collect like terms.
    • Expand expressions using the distributive property.
    • Categorize linear equations in one variable as having one, none, or infinitely many solutions.
    It also aims to encourage discussion on some common misconceptions about algebra.
Original Student Tutorials
Perspectives Video: Expert
Perspectives Video: Teaching Ideas
Problem-Solving Tasks
  • Ice Cream Van # In this open-ended problem-solving task, students are presented with a variety of constraints and are challenged to determine the break-even point using a method of their choice. Students will have to brainstorm or research several relevant quantities and incorporate these values into their solutions.
  • Guess My Number # This problem asks the students to represent a sequence of operations using an expression and then to write and solve simple equations. The problem is posed as a game and allows the students to visualize mathematical operations. It would make sense to actually play a similar game in pairs first and then ask the students to record the operations to figure out each other's numbers.
  • Baseball Cards # This task could be put to good use in an instructional sequence designed to develop knowledge related to students' understanding of linear functions in contexts. Though students could work independently on the task, collaboration with peers is more likely to result in the exploration of a range of interpretations.
  • Paying the Rent # Students solve problems tracking the balance of a checking account used only to pay rent. Students will write an equation to represent the given information, fill in a table of values, graph the equation, and use the graph to determine when the savings account reaches a determined goal. This simple conceptual task focuses on what it means for a number to be a solution to an equation, rather than on the process of solving equations.
  • Planes and Wheat # Students practice setting up equations using real-world government expenses. The emphasis is on setting up, rather than solving, the equations.
Tutorials
Unit/Lesson Sequence
  • Variables and Patterns of Change: Translating Words Into Symbols; Linear Equations # Lesson Plan 1: Miles of Tiles - The Pool Border Problem, students will recognize patterns and represent situations using algebraic notation and variables. Lesson Plan 2: Cups and Chips - Solving Linear Equations Using Manipulatives, students use manipulatives to represent visually the steps they take to obtain a solution to an algebraic equation. They develop an understanding of the connections between the solution involving manipulatives and the symbolic solution. Students work in teams of four. Site includes a Topic Overview, Lesson Plans, Student Work, Teaching Strategies, Resources, and a video of Workshop 1; Part 1.
Video/Audio/Animations
  • Solving Motion Problems with Linear Equations # Based upon the definition of speed, linear equations can be created which allow us to solve problems involving constant speeds, time, and distance. Note: This video exceeds basic expectations for the mathematical concept(s) at this grade level. The video is intended for students who have demonstrated mastery within the scope of instruction who may be ready for a more rigorous extension of the mathematical concept(s). As with all materials, ensure to gauge the readiness of students or adapt according to student's needs prior to administration.
  • Solving Problems with Linear Equations # The video explains the process of creating linear equations to solve real-world problems. 
MFAS Formative Assessments
  • Algebra or Arithmetic? # Students are asked to compare an arithmetic solution to an algebraic solution of a word problem.
  • Solve Equations # Students are asked to solve two equations involving rational numbers.
  • Squares # Students are asked to write and solve an equation of the form p(x + q) = r in the context of a problem about the perimeter of a square.
  • Write and Solve an Equation # Students are asked to write and solve a two-step equation to model the relationship among variables in a given scenario.
Original Student Tutorials Science - Grades K-8
  • Balancing the Machine # Use models to solve balance problems on a space station in this interactive, math and science tutorial. 
Original Student Tutorials Mathematics - Grades 6-8
Printed On:10/21/2025 8:05:51 PM
Print Page | Close this window