Remarks
Geometry - Fluency RecommendationsFluency with the use of construction tools, physical and computational, helps students draft a model of a geometric phenomenon and can lead to conjectures and proofs.
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
-
Also assesses:
- Assessment Limits :
Constructions are limited to copying a segment; copying an angle;
bisecting a segment; bisecting an angle; constructing perpendicular
lines, including the perpendicular bisector of a line segment;
constructing a line parallel to a given line through a point not on the
line; constructing an equilateral triangle inscribed in a circle;
constructing a square inscribed in a circle; and a regular hexagon
inscribed in a circle.Constructions are limited to the use of a formal compass and a
straightedge.Items should not ask student to find values or use properties of the
geometric figure that is constructed. - Calculator :
Neutral
- Clarification :
Students will identify the result of a formal geometric construction.Students will determine the steps of a formal geometric construction
- Stimulus Attributes :
Items may be set in a real-world or mathematical context. - Response Attributes :
Items may require the student to justify why a construction results in
the geometric figure.Items may require the student to use or choose the correct unit of
measure.Items may require the student to provide steps for a construction.
MAFS.912.G-CO.4.13
- Test Item #: Sample Item 1
- Question:
Ruben carries out a construction using Triangle BC. Click the play button to see a part of his construction,
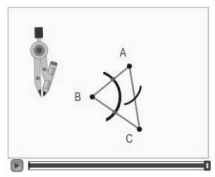
What will be the result of Ruben's construction?
- Difficulty: N/A
- Type: MC: Multiple Choice
Related Courses
Related Access Points
Related Resources
Formative Assessments
Lesson Plans
Original Student Tutorials
Presentation/Slideshow
Problem-Solving Tasks
Unit/Lesson Sequence
Video/Audio/Animation
MFAS Formative Assessments
Students are asked to construct the bisectors of a given segment and a given angle and to justify one of the steps in each construction.
Students are asked to construct an angle congruent to a given angle.
Students are asked to construct a line segment congruent to a given line segment.
Students are asked to construct a line parallel to a given line through a given point.
Students are asked to construct a line perpendicular to given line (1) through a point not on the line and (2) through a point on the line.
Original Student Tutorials Mathematics - Grades 9-12
Explore the construction processes for constructing an angle bisector, copying an angle and constructing a line parallel to a given line through a point not on the line using a variety of tools in this interactive, retro video game-themed tutorial.
NOTE: This tutorial uses both the angle bisector construction and the construction to copy an angle as an extension opportunity to also construct a line parallel to a given line through a point not on the line. Students also learn to identify corresponding angles created when a transversal crosses parallel lines, and discover using Geogebra that these angles are congruent.
Plan a paddle board expedition by learning how to do basic geometric constructions including copying a segment, constructing a segment bisector, constructing a segment's perpendicular bisector and constructing perpendicular segments using a variety of tools in this interactive tutorial.
Learn to construct the perpendicular bisector of a line segment using a straightedge and compass with this interactive tutorial.
Student Resources
Original Student Tutorials
Explore the construction processes for constructing an angle bisector, copying an angle and constructing a line parallel to a given line through a point not on the line using a variety of tools in this interactive, retro video game-themed tutorial.
NOTE: This tutorial uses both the angle bisector construction and the construction to copy an angle as an extension opportunity to also construct a line parallel to a given line through a point not on the line. Students also learn to identify corresponding angles created when a transversal crosses parallel lines, and discover using Geogebra that these angles are congruent.
Type: Original Student Tutorial
Plan a paddle board expedition by learning how to do basic geometric constructions including copying a segment, constructing a segment bisector, constructing a segment's perpendicular bisector and constructing perpendicular segments using a variety of tools in this interactive tutorial.
Type: Original Student Tutorial
Learn to construct the perpendicular bisector of a line segment using a straightedge and compass with this interactive tutorial.
Type: Original Student Tutorial
Presentation/Slideshow
This lesson teaches students about the history of the Pythagorean theorem, along with proofs and applications. It is geared toward high school Geometry students that have completed a year of Algebra and addresses the following national standards of the National Council of Teachers of Mathematics and the Mid-continent Research for Education and Learning: 1) Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships; 2) Use visualization, spatial reasoning, and geometric modeling to solve problems; 3) Understand and apply basic and advanced properties of the concepts of geometry; and 4) Use the Pythagorean theorem and its converse and properties of special right triangles to solve mathematical and real-world problems. The video portion is about thirty minutes, and with breaks could be completed in 50 minutes. (You may consider completing over two classes, particularly if you want to allow more time for activities or do some of the enrichment material). These activities could be done individually, in pairs, or groups. I think 2 or 3 students is optimal. The materials required for the activities include scissors, tape, string and markers.
Type: Presentation/Slideshow
Problem-Solving Tasks
This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context.
Type: Problem-Solving Task
This problem solving task challenges students to construct a perpendicular bisector of a given segment.
Type: Problem-Solving Task
This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected.
Type: Problem-Solving Task
This problem solving task challenges students to bisect a given angle.
Type: Problem-Solving Task
This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines).
Type: Problem-Solving Task
This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts.
Type: Problem-Solving Task
Parent Resources
Problem-Solving Tasks
This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context.
Type: Problem-Solving Task
This problem solving task challenges students to construct a perpendicular bisector of a given segment.
Type: Problem-Solving Task
This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected.
Type: Problem-Solving Task
This problem solving task challenges students to bisect a given angle.
Type: Problem-Solving Task
This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines).
Type: Problem-Solving Task
This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts.
Type: Problem-Solving Task