Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
- Assessment Limits :
In items that require the student to write an equation as a constraint, the equation may be a linear function.In items that require the student to write a system of equations to represent a constraint, the system is limited to two variables.
In items that require the student to write a system of inequalities to represent a constraint, the system is limited to two variables
- Calculator :
Neutral
- Clarification :
Students will write constraints for a real-world context using equations, inequalities, a system of equations, or a system of inequalities.Students will interpret the solution of a real-world context as viable or not viable.
- Stimulus Attributes :
Items must be set in a real-world context.Items may use function notation.
- Response Attributes :
Items may require the student to choose an appropriate level of accuracy.Items may require the student to choose and interpret the scale in a graph.
Items may require the student to choose and interpret units. Items may require the student to apply the basic modeling cycle.
- Test Item #: Sample Item 1
- Question:
The production cost, C, in thousands of dollars, for a toy company to manufacture a ball is given by the model C(x)=75+21x-0.72x², where x is the number of balls produced in one day, in thousands. The company wants to keep its production cost at or below $125,000. The graph shown models the situation.
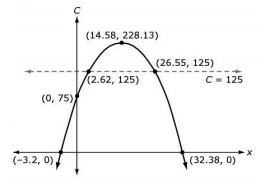
What is a reasonable constraint for the model?
- Difficulty: N/A
- Type: MC: Multiple Choice
Related Courses
Related Access Points
Related Resources
Formative Assessments
Lesson Plans
Original Student Tutorials
Perspectives Video: Expert
Perspectives Video: Professional/Enthusiasts
Problem-Solving Tasks
Unit/Lesson Sequence
Video/Audio/Animation
STEM Lessons - Model Eliciting Activity
The Alternative Fuel Systems MEA provides students with an engineering problem in which they must develop a procedure to decide the appropriate course for an automobile manufacturer to take given a set of constraints. The main focus of the MEA is to apply the concepts of work and energy to a business model.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.
The topic of this MEA is work and power. Students will be assigned the task of hiring employees to complete a given task. In order to make a decision as to which candidates to hire, the students initially must calculate the required work. The power each potential employee is capable of, the days they are available to work, the percentage of work-shifts they have missed over the past 12 months, and the hourly pay rate each worker commands will be provided to assist in the decision process. Full- and/or part-time positions are available. Through data analysis, the students will need to evaluate which factors are most significant in the hiring process. For instance, some groups may prioritize speed of work, while others prioritize cost or availability/dependability.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom.
The focus of this MEA is oil spills and their effect on the environment. In this activity, students from a fictitious class are studying about the effects of an oil spill on marine ecosystems and have performed an experiment in which they were asked to try to rid a teaspoon of corn oil from a baking pan filled with two liters of water as thoroughly as possible in a limited timeframe and with limited resources. By examining, analyzing, and evaluating experimental data related to resource usage, disposal, and labor costs, students must face the tradeoffs that are involved in trying to preserve an ecosystem when time, money, and resources are limited.
MFAS Formative Assessments
Students are asked to determine the constraint on a profit equation and to interpret solutions as being viable or not in the context of the problem.
Students are asked to represent constraints using inequalities given in a problem context.
Original Student Tutorials Mathematics - Grades 9-12
Learn how to solve and graph compound inequalities and determine if solutions are viable in part 2 of this interactive tutorial series.
Click HERE to open Part 1.
Learn how to solve and graph one variable inequalities, including compound inequalities, in part 1 of this interactive tutorial series.
Click HERE to open Part 2.
Learn how to create systems of linear equations to represent contextual situations in this interactive tutorial.
This part 6 in a 7-part series. Click below to explore the other tutorials in the series.
- Part 1: Solving Systems of Linear Equations: Using Graphs
- Part 2: Solving Systems of Linear Equations: Substitution
- Part 3: Solving Systems of Linear Equations: Basic Elimination
- Part 4: Solving Systems of Linear Equations: Advanced Elimination
- Part 5: Solving Systems of Linear Equations: Connecting Algebraic Methods to Graphing
- Part 7: Solving Systems of Linear Equations: Word Problems (Coming soon)
Student Resources
Original Student Tutorials
Learn how to create systems of linear equations to represent contextual situations in this interactive tutorial.
This part 6 in a 7-part series. Click below to explore the other tutorials in the series.
- Part 1: Solving Systems of Linear Equations: Using Graphs
- Part 2: Solving Systems of Linear Equations: Substitution
- Part 3: Solving Systems of Linear Equations: Basic Elimination
- Part 4: Solving Systems of Linear Equations: Advanced Elimination
- Part 5: Solving Systems of Linear Equations: Connecting Algebraic Methods to Graphing
- Part 7: Solving Systems of Linear Equations: Word Problems (Coming soon)
Type: Original Student Tutorial
Learn how to solve and graph compound inequalities and determine if solutions are viable in part 2 of this interactive tutorial series.
Click HERE to open Part 1.
Type: Original Student Tutorial
Learn how to solve and graph one variable inequalities, including compound inequalities, in part 1 of this interactive tutorial series.
Click HERE to open Part 2.
Type: Original Student Tutorial
Perspectives Video: Expert
<p>It's important to stay inside the lines of your project constraints to finish in time and under budget. This NASA systems engineer explains how constraints can actually promote creativity and help him solve problems!</p>
Type: Perspectives Video: Expert
Problem-Solving Tasks
The given solutions for this task involve the creation and solving of a system of two equations and two unknowns, with the caveat that the context of the problem implies that we are interested only in non-negative integer solutions. Indeed, in the first solution, we must also restrict our attention to the case that one of the variables is further even. This aspect of the task is illustrative of the mathematical practice of modeling with mathematics, and crucial as the system has an integer solution for both situations, that is, whether we include the dollar on the floor in the cash box or not.
Type: Problem-Solving Task
The purpose of this task is to give students practice writing a constraint equation for a given context. Instruction accompanying this task should introduce the notion of a constraint equation as an equation governing the possible values of the variables in question (i.e., "constraining" said values). In particular, it is worth differentiating the role of constraint equations from more functional equations, e.g., formulas to convert from degrees Celsius to degree Fahrenheit. The task has students interpret the context and choose variables to represent the quantities, which are governed by the constraint equation and the fact that they are non-negative (allowing us to restrict the graphs to points in the first quadrant only).
The four parts are independent and can be used as separate tasks.
Type: Problem-Solving Task
This task presents a simple but mathematically interesting game whose solution is a challenging exercise in creating and reasoning with algebraic inequalities. The core of the task involves converting a verbal statement into a mathematical inequality in a context in which the inequality is not obviously presented, and then repeatedly using the inequality to deduce information about the structure of the game.
Type: Problem-Solving Task
Students are given a word problem that can be solved by using a pair of linear equations. This task does not actually require that the student solve the system but that they recognize the pairs of linear equations in two variables that would be used to solve the system. This is an important step in the process of solving systems.
Type: Problem-Solving Task
This task is designed to make students think about the meaning of the quantities presented in the context and choose which ones are appropriate for the two different constraints presented. In particular, note that the purpose of the task is to have students generate the constraint equations for each part (though the problem statements avoid using this particular terminology), and not to have students solve said equations. If desired, instructors could also use this task to touch on such solutions by finding and interpreting solutions to the system of equations created in parts (a) and (b).
Type: Problem-Solving Task
Video/Audio/Animation
This video demonstrates writing a function that represents a real-life scenario.
Type: Video/Audio/Animation
Parent Resources
Perspectives Video: Expert
<p>It's important to stay inside the lines of your project constraints to finish in time and under budget. This NASA systems engineer explains how constraints can actually promote creativity and help him solve problems!</p>
Type: Perspectives Video: Expert
Problem-Solving Tasks
The given solutions for this task involve the creation and solving of a system of two equations and two unknowns, with the caveat that the context of the problem implies that we are interested only in non-negative integer solutions. Indeed, in the first solution, we must also restrict our attention to the case that one of the variables is further even. This aspect of the task is illustrative of the mathematical practice of modeling with mathematics, and crucial as the system has an integer solution for both situations, that is, whether we include the dollar on the floor in the cash box or not.
Type: Problem-Solving Task
The purpose of this task is to give students practice writing a constraint equation for a given context. Instruction accompanying this task should introduce the notion of a constraint equation as an equation governing the possible values of the variables in question (i.e., "constraining" said values). In particular, it is worth differentiating the role of constraint equations from more functional equations, e.g., formulas to convert from degrees Celsius to degree Fahrenheit. The task has students interpret the context and choose variables to represent the quantities, which are governed by the constraint equation and the fact that they are non-negative (allowing us to restrict the graphs to points in the first quadrant only).
The four parts are independent and can be used as separate tasks.
Type: Problem-Solving Task
This task presents a simple but mathematically interesting game whose solution is a challenging exercise in creating and reasoning with algebraic inequalities. The core of the task involves converting a verbal statement into a mathematical inequality in a context in which the inequality is not obviously presented, and then repeatedly using the inequality to deduce information about the structure of the game.
Type: Problem-Solving Task
Students are given a word problem that can be solved by using a pair of linear equations. This task does not actually require that the student solve the system but that they recognize the pairs of linear equations in two variables that would be used to solve the system. This is an important step in the process of solving systems.
Type: Problem-Solving Task
This task is designed to make students think about the meaning of the quantities presented in the context and choose which ones are appropriate for the two different constraints presented. In particular, note that the purpose of the task is to have students generate the constraint equations for each part (though the problem statements avoid using this particular terminology), and not to have students solve said equations. If desired, instructors could also use this task to touch on such solutions by finding and interpreting solutions to the system of equations created in parts (a) and (b).
Type: Problem-Solving Task