
|
Generated on 9/13/2025 at 12:47 AM |
The webpage this document was printed/exported from can be found at the following URL:
https://www.cpalms.org/PreviewIdea/Preview/1498
https://www.cpalms.org/PreviewIdea/Preview/1498
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Standard 1 : Work with radicals and integer exponents. (Major Cluster)Archived
Cluster Standards
This cluster includes the following benchmarks.
Visit the specific benchmark webpage to find related instructional resources.
- MAFS.8.EE.1.1 : Know and apply the properties of integer exponents to generate
equivalent numerical expressions. For example, 3² ×
 =
=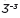 =1/3³=1/27.
=1/3³=1/27. - MAFS.8.EE.1.2 : Use square root and cube root symbols to represent solutions to equations of the form x² = p and x³ = p, where p is a positive rational number. Evaluate square roots of small perfect squares and cube roots of small perfect cubes. Know that √2 is irrational.
- MAFS.8.EE.1.3 : Use numbers expressed in the form of a single digit times an integer
power of 10 to estimate very large or very small quantities, and to
express how many times as much one is than the other. For example,
estimate the population of the United States as 3 ×
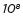 and the population
of the world as 7 ×
and the population
of the world as 7 × 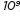 , and determine that the world population is more
than 20 times larger.
, and determine that the world population is more
than 20 times larger. - MAFS.8.EE.1.4 : Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used. Use scientific notation and choose units of appropriate size for measurements of very large or very small quantities (e.g., use millimeters per year for seafloor spreading). Interpret scientific notation that has been generated by technology.
Cluster Information
Number:
MAFS.8.EE.1
Title:
Work with radicals and integer exponents. (Major Cluster)
Type:
Cluster
Subject:
Mathematics - Archived
Grade:
8
Domain-Subdomain
Expressions & Equations
Cluster Access Points
This cluster includes the following Access Points.
- MAFS.8.EE.1.AP.3a : Multiply single digits by the power of 10 using a calculator.
- MAFS.8.EE.1.AP.1a : Use properties of integer exponents to produce equivalent expressions.
- MAFS.8.EE.1.AP.2a : Use appropriate tools to calculate square root and cube root.
- MAFS.8.EE.1.AP.2b : Find products when bases from -6 to 6 are squared and cubed, using a calculator.
- MAFS.8.EE.1.AP.2c : Identify perfect squares from 0 to 100 by modeling them on graph paper or building with tiles.
- MAFS.8.EE.1.AP.2d : Identify squares and cubes as perfect or non-perfect.
- MAFS.8.EE.1.AP.2e : Recognize that non-perfect squares/cubes are irrational.
- MAFS.8.EE.1.AP.3b : Identify the products of powers of 10 (through 108).
- MAFS.8.EE.1.AP.4a : Perform operations with numbers expressed in scientific notation using a calculator.
Cluster Resources
Vetted resources educators can use to teach the concepts and skills in this topic.
Original Student Tutorials
- Modelling The Solar System Part 2: Scientific Notation: Use scientific notation to compare the distances of planets and other objects from the Sun in this interactive tutorial.
- Modelling the Solar System Part 1: Astronomical Units: Use astronomical units to compare distances betweeen objects in our solar system in this interactive tutorial.
- Square Root Part 3: Simplifying Radicals: Learn how to simplify radicals in this interactive tutorial.
- Square Root Part 2: Non-Perfect Squares: Learn what non-perfect squares are and find the decimal approximation of their square roots in this interactive tutorial.
- Square Root Part 1: Perfect Squares: Learn what perfect squares are and find their square roots in this interactive tutorial.
- Scientific Notation: Expressing Large Quantities: Explore how to express large quantities using scientific notation in this interactive tutorial.
Formative Assessments
- Roots and Radicals: Students are asked to solve simple quadratic and cubic equations and represent solutions using square root and cube root symbols.
- Equivalent Powers Expressions: Students are given numerical expressions and asked to use properties of integer exponents to find equivalent expressions.
- Exponents Tabled: Students are asked to complete a table of powers of three and provide an explanation of zero powers.
- The Root of the Problem: Students are asked to evaluate perfect square roots and perfect cube roots.
- Sums and Differences in Scientific Notation: Students are asked to add and subtract numbers given in scientific notation in real-world contexts.
- Scientific Multiplication and Division: Students are asked to multiply and divide numbers given in scientific notation in real-world contexts.
- Mixed Form Operations: Students are given word problems with numbers in both standard and scientific notation and asked to solve problems using various operations.
- Estimating Length Using Scientific Notation: This lesson unit is intended to help you assess how well students are able to:
- Estimate lengths of everyday objects.
- Convert between decimal and scientific notation.
- Make comparisons of the size of numbers expressed in both decimal and scientific notation.
- Multiplying and Dividing Integer Exponents: Students are asked to apply the properties of integer exponents to generate equivalent numerical expressions.
- Dimensions Needed: Students are asked to solve problems involving square roots and cube roots.
- Estimating Extreme Values: Students are asked to estimate an extremely large and an extremely small number by writing it in the form a x
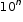 .
. - Order Matters: Students are given pairs of numbers written in the form of an integer times a power of 10 and are asked to compare the numbers in each pair using the inequality symbols.
- How Many Times?: Students are given pairs of numbers written in exponential form and are asked to compare them multiplicatively.
- Compare Numbers: Students are given pairs of numbers written in scientific notation and are asked to compare them multiplicatively.
- Negative Exponential Expressions: Students are given expressions with negative exponents and are asked to identify those that are equivalent from given sets of expressions.
- Scientific Calculator Display: Students are given examples of calculator displays and asked to convert the notation in the display to both scientific notation and standard form.
Lesson Plans
- Which Map Should We Use?: Students will create a working model of the solar system to scale. They will incorporate QR codes to present information on solar system objects, as well as compare the geocentric and heliocentric models of the solar system.
- How Many Smoots Does It Take to Reach the Moon?: In this discovery oriented lesson, students will explore the use of non-standard units of measurement. They will convert linear measurements within the metric system and convert measurements given in astronomical units (AU) into more familiar units, specifically meters and kilometers. The unit conversions will be completed with measurements that are expressed in scientific notation. Students will recall their prior knowledge of how to add and subtract numbers given in scientific notation. They will also use their knowledge of exponent rules to determine an efficient method for multiplying and dividing numbers expressed in scientific notation.
- Generalizing Patterns: The Difference of Two Squares: This lesson is designed to help teachers assess how well students can work with square numbers. Upon completion of the lesson, students should be able to describe and explain their findings and why results are possible or impossible. This lesson is a bridge towards proofs. The materials required for this lesson are worksheets, plain paper, large sheets of paper for making posters, and felt-tip pens. The entire lesson requires 110 minutes, broken down into a 20-minute pre-lesson, an 80-minute lesson (or two 40-minute lessons), and a 10-minute follow-up lesson.
- Estimating Length Using Scientific Notation: This lesson unit is intended to help you assess how well students are able to estimate lengths of everyday objects, convert between decimal and scientific notation and make comparisons of the size of numbers expressed in both decimal and scientific notation.
- Multiplying terms that have the same base: Students explore numerical examples involving multiplying exponential terms that have the same base. They generalize the property of exponents where, when multiplying terms with the same base, the base stays the same and the exponents are added together.
- Operating with Exponents!: Students will participate in a gallery walk in which they observe patterns in algebraic expressions. Students will apply the properties of integer exponents to simplify expressions.
- Discovering Kepler's Law for the Periods of Planets: Students listen to a video that describes Kepler's determination that planetary orbits are elliptical and then will use data for the solar distance and periods of several of the planets in the solar system, then investigate several hypotheses to determine which is supported by the data.
- Stand Up for Negative Exponents: This low-tech lesson will have students stand up holding different exponent cards. This will help them write and justify an equivalent expression and see the pattern for expressions with the same base and descending exponents. What happens as you change from 2 to the fourth power to 2 to the third power; 2 to the second power; and so forth? This is an introductory lesson to two of the properties of exponents:
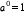 and
and 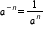
- Scavenger Hunt for Multiplying and Dividing Powers: Get your students up and moving and interested in simplifying expressions with whole integer powers. After getting your students to figure out what it takes to multiply and divide powers with whole number exponents, have your students scurry about the room to find the questions and answers for scavenger hunt exercise. The lesson includes questions and answers for the hunt, directions for the hunt, printable cards for the hunt, and step by step directions on how to get your students to figure out what they need to do when multiplying and dividing powers with whole number exponents.
- Math Is Exponentially Fun!: The students will informally learn the rules for exponents: product of powers, powers of powers, zero and negative exponents. The activities provide the teacher with a progression of steps that help lead students to determine results without knowing the rules formally. The closing activity is hands-on to help reinforce all rules.
- Multiplying with Common Bases: This resource provides a Lesson Plan for teaching students how to apply the Product of Powers Property of exponents. They will be able to write equivalent exponential expressions and evaluate them when possible.
- Exponential Chips: In this lesson students will learn the properties of integer exponents and how to apply them to multiplication and division. Students will have the opportunity to work with concrete manipulatives to create an understanding of these properties and then apply them abstractly. The students will also develop the understanding of the value of any integer with a zero exponent.
Problem-Solving Tasks
- Ponzi Scheme Pondering: The students must rationalize how a Ponzi email could make money or fall apart. Using their knowledge of exponential growth, the students can estimate the potential gains, but then are asked to think about why these schemes are illegal and tend to collapse.
- Pennies to Heaven: The goal of this task is to give students a context to investigate large numbers and measurements. Students need to fluently convert units with very large numbers in order to successfully complete this task. The total number of pennies minted either in a single year or for the last century is phenomenally large and difficult to grasp. One way to assess how large this number is would be to consider how far all of these pennies would reach if we were able to stack them one on top of another: this is another phenomenally large number but just how large may well come as a surprise.
- Ant and Elephant: In this problem students are comparing a very small quantity with a very large quantity using the metric system. The metric system is especially convenient when comparing measurements using scientific notations since different units within the system are related by powers of ten.
- Ants versus humans: This task requires students to work with very large and small values expressed both in scientific notation and in decimal notation (standard form). In addition, students need to convert units of mass. The solution below converts the mass of humans into grams; however, we could just as easily converted the mass of ants into kilograms. Students are unable to go directly to a calculator without taking into account all of the considerations mentioned above. Even after converting units and decimals to scientific notation, students should be encouraged to use the structure of scientific notation to regroup the products by extending the properties of operations and then use the properties of exponents to more fluently perform the calculations involved rather than rely heavily on a calculator.
- Giantburgers: The student is asked to perform operations with numbers expressed in scientific notation to decide whether 7% of Americans really do eat at Giantburger every day.
- Extending the Definitions of Exponents, Variation 1: This is an instructional task meant to generate a conversation around the meaning of negative integer exponents. It is good for students to learn the convention that negative time is simply any time before t=0.
Student Center Activity
- Edcite: Mathematics Grade 8: Students can practice answering mathematics questions on a variety of topics. With an account, students can save their work and send it to their teacher when complete.
Tutorials
- Limits and Infinity: We will look at examples of limits at infinity.
- Exponent Properties Involving Products: This video discusses exponent properties involving products.
- Exponent Properties Involving Quotients: This video models how to use the Quotient of Powers property.
- Multiplying in Scientific Notation: This video demonstrates multiplying in scientific notation.
- Calculating Red Blood Cells in the Body Using Scientific Notation: This example demonstrates mathematical operations with scientific notation used to solve a word problem.
- Negative exponents: This tutorial shows students the rule for negative exponents. Students will see, using variables, the pattern for negative exponents.
- U.S. National Debt (Scientific Notation Word Problem): This video demonstrates a scientific notation word problem involving division.
- Simplifying an Expression into Scientific Notation: This is an example showing how to simplify an expression into scientific notation.
- Negative exponents: In this tutorial, students will learn about negative exponents. An emphasis is placed on multiplying by the reciprocal of a number.
- Finding the square root of a decimal: Students will learn how to find the square root of a decimal number.
- Finding cube roots: Learn how to find the cube root of -512 using prime factorization.
- Introduction to cube roots: Students will learn the meaning of cube roots and how to find them. Students will also learn how to find the cube root of a negative number.
- Introduction to square roots: Students will earn about the square root symbol (the principal root) and what it means to find a square root. Students will also learn how to solve simple square root equations.
- Exponents with Negative Bases: In this tutorial, you will apply what you know about multiplying negative numbers to determine how negative bases with exponents are affected and what patterns develop.
- Exponents and Powers: This tutorial reviews the concept of exponents and powers and includes how to evaluate powers with negative signs.
- Power of a Power Property: This tutorial demonstrates how to use the power of a power property with both numerals and variables.
- Raising Exponential Expressions to Powers: If a term raised to a power is enclosed in parentheses and then raised to another power, this expression can be simplified using the rules of multiplying exponents.
- Raising Products and Quotients to Powers: Any expression consisting of multiplied and divide terms can be enclosed in parentheses and raised to a power. This can then be simplified using the rules for multiplying exponents.
- Scientific Notation: Scientific notation is used to conveniently write numbers that require many digits in their representations. How to convert between standard and scientific notation is explained in this tutorial.
Video/Audio/Animations
- Exponentiation: Exponentiation can be understood in terms of repeated multiplication much like multiplication can be understood in terms of repeated addition. Properties of multiplication and division of exponential expressions with the same base are derived.
- Exponents of One, Zero, and Negative: Integer exponents greater than one represent the number of copies of the base which are multiplied together. hat if the exponent is one, zero, or negative? Using the rules of adding and subtracting exponents, we can see what the meaning must be.
- Simplifying Multiplied Exponential Expressions: Exponential expressions with multiplied terms can be simplified using the rules for adding exponents.
- Simplifying Divided Exponential Expressions: Exponential expressions with divided terms can be simplified using the rules for subtracting exponents.
- Simplifying Mixed Exponential Expressions: Exponential expressions with multiplied and divided terms can be simplified using the rules of adding and subtracting exponents.