- MAFS.912.A-SSE.2.3:
Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.★
- Factor a quadratic expression to reveal the zeros of the function it defines.
- Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.
- Use the properties of exponents to transform expressions for exponential functions. For example the expression
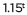 can be rewritten as
can be rewritten as 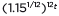 ≈
≈ 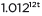 to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.
to reveal the approximate equivalent monthly interest rate if the annual rate is 15%.

|
Generated on 8/28/2025 at 3:52 PM |
https://www.cpalms.org/PreviewAccessPoint/Preview/16107
Essential Understandings
Concrete:
- Use a tool to determine whether the quadratic function crosses the x-axis. Click Here
- Use a graphing tool or graphing software to find the roots (where the function intersects the x-axis) of a function.
- Use manipulatives (i.e. algebra tiles) to simplify or to write equivalent forms of quadratic functions.
- Use algebra tiles or manipulatives to complete the square.
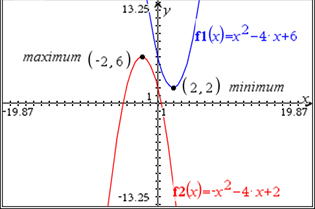
Youtube: Click Here - Use the graph of the quadratic equation to identify the vertex of the function.
- Identify the maximum or minimum of the graph of the quadratic equation.
- Understand the following concepts and vocabulary: root, factor, quadratic, integer, real number, quadratic equation, quadratic formula, square root, solution, terms, coefficient, intercept, intersect, zero, completing the square, vertex form, maximum, minimum, vertex, trinomial.
- Use steps or a template to complete the square.

- Understand quadratic equations can be rewritten in vertex form
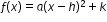 .
. - Understand that the vertex of a quadratic function is represented by (h, k). The vertex of a quadratic function is the maximum/minimum coordinate of the function. If the function opens up it is a minimum, if the function opens down it is a maximum.
For example: y=3(x+2)2-4 (Vertex form)
Vertex (h, k) = (-2, 4)
The vertex will be moved 2 units to the left and 4 units up from (0,0), the vertex of the parent function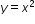 .
. - Teacher tool: Click Here
- MathBitsNotebook: Click Here
Visit the specific benchmark webpage to find related instructional resources.
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
- Algebra 1 (#1200310): In Algebra 1, instructional time will emphasize five areas: (1) performing operations with polynomials and radicals, and extending the Laws of Exponents to include rational exponents; (2) extending understanding of functions to linear, quadratic and exponential functions and using them to model and analyze real-world relationships; (3) solving quadratic equations in one variable and systems of linear equations and inequalities in two variables; (4) building functions, identifying their key features and representing them in various ways and (5) representing and interpreting categorical and numerical data with one and two variables.
All clarifications stated, whether general or specific to Algebra I, are expectations for instruction of that benchmark.
Curricular content for all subjects must integrate critical-thinking, problem-solving, and workforce-literacy skills; communication, reading, and writing skills; mathematics skills; collaboration skills; contextual and applied-learning skills; technology-literacy skills; information and media-literacy skills; and civic-engagement skills.
- Algebra 1 Honors (#1200320): In Algebra 1 Honors, instructional time will emphasize five areas: (1) performing operations with polynomials and radicals, and extending the Laws of Exponents to include rational exponents; (2) extending understanding of functions to linear, quadratic and exponential functions and using them to model and analyze real-world relationships; (3) solving quadratic equations in one variable and systems of linear equations and inequalities in two variables; (4) building functions, identifying their key features and representing them in various ways and (5) representing and interpreting categorical and numerical data with one and two variables.
All clarifications stated, whether general or specific to Algebra I Honors, are expectations for instruction of that benchmark.
Curricular content for all subjects must integrate critical-thinking, problem-solving, and workforce-literacy skills; communication, reading, and writing skills; mathematics skills; collaboration skills; contextual and applied-learning skills; technology-literacy skills; information and media-literacy skills; and civic-engagement skills.
- Algebra 2 (#1200330): In Algebra 2, instructional time will emphasize five areas: (1) extending arithmetic operations with algebraic expressions to include radical and rational expressions and polynomial division; (2) graphing and analyzing functions including polynomials, absolute value, radical, rational, exponential and logarithmic; (3) building functions using compositions, inverses and transformations; (4) extending systems of equations and inequalities to include non-linear expressions and (5) developing understanding of the complex number system, including complex numbers as roots of polynomial equations.
All clarifications stated, whether general or specific to Algebra 2, are expectations for instruction of that benchmark
Curricular content for all subjects must integrate critical-thinking, problem-solving, and workforce-literacy skills; communication, reading, and writing skills; mathematics skills; collaboration skills; contextual and applied-learning skills; technology-literacy skills; information and media-literacy skills; and civic-engagement skills.
- Algebra 2 Honors (#1200340): In Algebra 2 Honors, instructional time will emphasize six areas: (1) developing understanding of the complex number system, including complex numbers as roots of polynomial equations; (2) extending arithmetic operations with algebraic expressions to include polynomial division, radical and rational expressions; (3) graphing and analyzing functions including polynomials, absolute value, radical, rational, exponential and logarithmic; (4) extending systems of equations and inequalities to include non-linear expressions; (5)building functions using compositions, inverses and transformations and (6) developing understanding of probability concepts.
All clarifications stated, whether general or specific to Algebra 2 Honors, are expectations for instruction of that benchmark.
Curricular content for all subjects must integrate critical-thinking, problem-solving, and workforce-literacy skills; communication, reading, and writing skills; mathematics skills; collaboration skills; contextual and applied-learning skills; technology-literacy skills; information and media-literacy skills; and civic-engagement skills.
- Algebra 1-B (#1200380): In Algebra 1-B, instructional time will emphasize four areas: (1) performing operations with polynomials and radicals, and extending the Laws of Exponents to include rational exponents; (2) extending understanding of functions to quadratic and exponential functions and using them to model and analyze real-world relationships; (3) solving quadratic equations in one variables and (4) building functions, identifying their key features and representing them in various ways.
All clarifications stated, whether general or specific to Algebra I-B, are expectations for instruction of that benchmark. Please note that all clarifications that address Algebra 1 also should be addressed within Algebra 1-B.
Curricular content for all subjects must integrate critical-thinking, problem-solving, and workforce-literacy skills; communication, reading, and writing skills; mathematics skills; collaboration skills; contextual and applied-learning skills; technology-literacy skills; information and media-literacy skills; and civic-engagement skills.
- Foundational Skills in Mathematics 9-12 (#1200400): This course supports students who need additional instruction in foundational mathematics skills as it relates to core instruction. Instruction will use explicit, systematic, and sequential approaches to mathematics instruction addressing all strands including number sense & operations, algebraic reasoning, functions, geometric reasoning and data analysis & probability. Teachers will use the listed benchmarks that correspond to each students’ needs.
Effective instruction matches instruction to the need of the students in the group and provides multiple opportunities to practice the skill and receive feedback. The additional time allotted for this course is in addition to core instruction. The intervention includes materials and strategies designed to supplement core instruction.
- Liberal Arts Mathematics (#1207310):
- Mathematics for College Success (#1200410):
- Mathematics for College Algebra (#1200700): This course is targeted for students who are not yet "college ready" in mathematics or simply need some additional instruction in content to prepare them for success in college level mathematics. This course incorporates the Florida Standards for Mathematical Practices as well as the following Florida Standards for Mathematical Content: Expressions and Equations, The Number System, Functions, Algebra, Geometry, Number and Quantity, Statistics and Probability, and the Florida Standards for High School Modeling. The standards align with the Mathematics Postsecondary Readiness Competencies deemed necessary for entry-level college courses.
English Language Development (ELD) Standards Special Notes Section:
Teachers are required to provide listening, speaking, reading and writing instruction that allows English Language Learners (ELL) to communicate information, ideas and concepts for academic success in the content area of Mathematics. For the given level of English language proficiency and with visual, graphic, or interactive support, students will interact with grade level words, expressions, sentences and discourse to process or produce language necessary for academic success. The ELD standard should specify a relevant content area concept or topic of study chosen by curriculum developers and teachers which maximize an ELL's need for communication and social skills. To access an ELL supporting document which delineates performance definitions and descriptors, please clock on the following link: {{AzureStorageLink}}/uploads/docs/standards/eld/ma.pdf.
For additional information on the development and implementation of the ELD standards, please contact the Bureau of Student Achievement through Language Acquisition at sala@fldoe.org.
Additional Instructional Resources:
A.V.E. for Success Collection is provided by the Florida Association of School Administrators: http://www.fasa.net/4DCGI/cms/review.html?Action=CMS_Document&DocID=139. Please be aware that these resources have not been reviewed by CPALMS and there may be a charge for the use of some of them in this collection.
- Access Informal Geometry (#7912060):
- Access Mathematics for Liberal Arts (#7912070): Access Courses:
Access courses are for students with the most significant cognitive disabilities. Access courses are designed to provide students access to grade-level general curriculum. Access points are alternate academic achievement standards included in access courses that target the salient content of Florida’s standards. Access points are intentionally designed to academically challenge students with the most significant cognitive disabilities.
- Access Algebra 1A (#7912080): Access Courses:
Access courses are for students with the most significant cognitive disabilities. Access courses are designed to provide students access to grade-level general curriculum. Access points are alternate academic achievement standards included in access courses that target the salient content of Florida’s standards. Access points are intentionally designed to academically challenge students with the most significant cognitive disabilities.
- Access Algebra 1B (#7912090): Access Courses:
Access courses are for students with the most significant cognitive disabilities. Access courses are designed to provide students access to grade-level general curriculum. Access points are alternate academic achievement standards included in access courses that target the salient content of Florida’s standards. Access points are intentionally designed to academically challenge students with the most significant cognitive disabilities.
- Algebra 1 for Credit Recovery (#1200315): Credit Recovery courses are credit bearing courses with specific content requirements defined by state academic standards (SAS). Students enrolled in a Credit Recovery course must have previously attempted the corresponding course (and/or End-of-Course assessment) since the course requirements for the Credit Recovery course is exactly the same as the previously attempted corresponding course. For example, Geometry (1206310) and Geometry for Credit Recovery (1206315) have identical content requirements. It is important to note that Credit Recovery courses are not bound by Section 1003.436(1) (a), Florida Statutes, requiring a minimum of 135 hours of bona fide instruction (120 hours in a school/district implementing block scheduling) in a designed course of study that contains student performance standards, since the students have previously attempted successful completion of the corresponding course. Additionally, Credit Recovery courses should ONLY be used for credit recovery, grade forgiveness, or remediation for students needing to prepare for an End-of-Course assessment retake.
In Algebra 1, instructional time will emphasize five areas: (1) performing operations with polynomials and radicals, and extending the Laws of Exponents to include rational exponents; (2) extending understanding of functions to linear, quadratic and exponential functions and using them to model and analyze real-world relationships; (3) solving quadratic equations in one variable and systems of linear equations and inequalities in two variables; (4) building functions, identifying their key features and representing them in various ways and (5) representing and interpreting categorical and numerical data with one and two variables.
All clarifications stated, whether general or specific to Algebra I, are expectations for instruction of that benchmark.
Curricular content for all subjects must integrate critical-thinking, problem-solving, and workforce-literacy skills; communication, reading, and writing skills; mathematics skills; collaboration skills; contextual and applied-learning skills; technology-literacy skills; information and media-literacy skills; and civic-engagement skills.
- Algebra 2 for Credit Recovery (#1200335): Special notes: Credit Recovery courses are credit bearing courses with specific content requirements defined by Next Generation Sunshine State Standards and/or Florida Standards. Students enrolled in a Credit Recovery course must have previously attempted the corresponding course (and/or End-of-Course assessment) since the course requirements for the Credit Recovery course are exactly the same as the previously attempted corresponding course. For example, Geometry (1206310) and Geometry for Credit Recovery (1206315) have identical content requirements. It is important to note that Credit Recovery courses are not bound by Section 1003.436(1)(a), Florida Statutes, requiring a minimum of 135 hours of bona fide instruction (120 hours in a school/district implementing block scheduling) in a designed course of study that contains student performance standards, since the students have previously attempted successful completion of the corresponding course. Additionally, Credit Recovery courses should ONLY be used for credit recovery, grade forgiveness, or remediation for students needing to prepare for an End-of-Course assessment retake.
- Algebra 1-B for Credit Recovery (#1200385): In Algebra 1-B, instructional time will emphasize four areas: (1) performing operations with polynomials and radicals, and extending the Laws of Exponents to include rational exponents; (2) extending understanding of functions to quadratic and exponential functions and using them to model and analyze real-world relationships; (3) solving quadratic equations in one variables and (4) building functions, identifying their key features and representing them in various ways.
All clarifications stated, whether general or specific to Algebra I-B, are expectations for instruction of that benchmark. Please note that all clarifications that address Algebra 1 also should be addressed within Algebra 1-B.
Curricular content for all subjects must integrate critical-thinking, problem-solving, and workforce-literacy skills; communication, reading, and writing skills; mathematics skills; collaboration skills; contextual and applied-learning skills; technology-literacy skills; information and media-literacy skills; and civic-engagement skills.
Special Notes: Credit Recovery courses are credit bearing courses with specific content requirements defined by state academic standards (SAS). Students enrolled in a Credit Recovery course must have previously attempted the corresponding course (and/or End-of-Course assessment) since the course requirements for the Credit Recovery course is exactly the same as the previously attempted corresponding course. For example, Geometry (1206310) and Geometry for Credit Recovery (1206315) have identical content requirements. It is important to note that Credit Recovery courses are not bound by Section 1003.436(1)(a), Florida Statutes, requiring a minimum of 135 hours of bona fide instruction (120 hours in a school/district implementing block scheduling) in a designed course of study that contains student performance standards, since the students have previously attempted successful completion of the corresponding course. Additionally, Credit Recovery courses should ONLY be used for credit recovery, grade forgiveness, or remediation for students needing to prepare for an End-of-Course assessment retake.
- Access Geometry (#7912065): Access Courses:
Access courses are for students with the most significant cognitive disabilities. Access courses are designed to provide students access to grade-level general curriculum. Access points are alternate academic achievement standards included in access courses that target the salient content of Florida’s standards. Access points are intentionally designed to academically challenge students with the most significant cognitive disabilities.
- Access Algebra 1 (#7912075): Access Courses:
Access courses are for students with the most significant cognitive disabilities. Access courses are designed to provide students access to grade-level general curriculum. Access points are alternate academic achievement standards included in access courses that target the salient content of Florida’s standards. Access points are intentionally designed to academically challenge students with the most significant cognitive disabilities.
- Access Algebra 2 (#7912095): Access Courses:
Access courses are for students with the most significant cognitive disabilities. Access courses are designed to provide students access to grade-level general curriculum. Access points are alternate academic achievement standards included in access courses that target the salient content of Florida’s standards. Access points are intentionally designed to academically challenge students with the most significant cognitive disabilities.
- Mathematics for Data and Financial Literacy (#1200387):