Standard #: MA.6.A.1.1 (Archived Standard)


This document was generated on CPALMS - www.cpalms.org



Explain and justify procedures for multiplying and dividing fractions and decimals.


Remarks


For division of fractions, students might use drawings, manipulatives, and symbolic notation to describe how and explain why they can find a common denominator and then divide just the numerators to find the quotient.

Example: In order to divide 2/3 by 1/4 , a student may reason that 2/3 = 8/12 and 1/4 = 3/12. So, (2/3)÷(1/4) is equivalent to (8/12)÷(3/12), which gives the same result as 8÷3=2 2/3. The following picture is a representation that matches the above explanation:

In the following fraction multiplication examples, students may use drawings or physical objects to represent the problems and explain their solution.

Example 1: One-half of your yard is garden. One- fourth of your garden is a vegetable garden. What fraction of your yard is a vegetable garden? Draw a picture and write a number sentence that both describe the problem and solution.

Pizza Parlor Scenarios

Example 2: A cook made four pizzas that had 3/5 of a package of mushrooms on each. How many packages of mushrooms were used?

 

Example 3: Sue ate some pizza. 2/3 of a pizza is left over. Jim ate 3/4 of the left over pizza. How much of a whole pizza did Jim eat?

Example 4: A party dessert pizza measures 2/3 of a yard by 3/4 of a yard. How much of a square yard is the party dessert pizza?

Example 5: There was 4/5 of a pound of pizza dough leftover in the freezer from the previous day. The cook thawed out 3/8 of the leftover dough. How much of a pound of dough did the cook thaw?

 

 



General Information

Subject Area: X-Mathematics (former standards - 2008)
Grade: 6
Body of Knowledge: Algebra
Big Idea: BIG IDEA 1 - Develop an understanding of and fluency with multiplication and division of fractions and decimals.
Date Adopted or Revised: 09/07
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived
Assessed: Yes

Test Item Specifications

    Item Type(s): This benchmark may be assessed using: MC item(s)
    N/A

    Clarification :
    Students may identify procedures for multiplying or dividing fractions and/or decimals in the context of expressions, equations, or real-world situations.

    Students will choose the correct graphic representation of multiplication or division problems involving fractions or decimals.
    Content Limits :
    Items may include mixed numbers, fractions, and/or decimals.

    Items may include decimals through the hundredths place.

    Denominators of fractions used must be less than or equal to 16.

    Items will not require the student to simplify fractions.

    Items may not include a combination of fractions and decimals.
    Stimulus Attributes :
    Items should be set in a real-world or mathematical context.

    Graphical representations of fractions, mixed numbers, and/or decimals may be used, as appropriate.


Sample Test Items (1)

Test Item # Question Difficulty Type
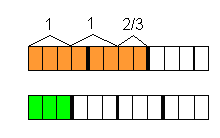
Sample Item 1 Merrill baked a cake in the shape of a rectangular prism for a party. After the party, 1/4 of the cake had not been eaten. Merrill froze 2/3 of the remaining cake. A diagram of the portion eaten and the portion frozen is shown below.

Cake Diagram

Which expression can be used to find the fraction of the original whole cake Merrill froze?

N/A MC: Multiple Choice


Related Resources

Lesson Plans

Name Description
Sandy's Candy Machine

In this Model Eliciting Activity (MEA), students will use the 4 operations with decimal numbers and calculate profit (including negative numbers) as well as use the resulting data to help a business owner make decisions about their candy stores.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student-centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

Dividing Fractions

In this lesson students will explore the different methods available for dividing fractions through a student-based investigation. The teacher will facilitate the discussion, but the students will discover the different methods on their own or with a partner as they work through the different steps.

Multiplying a Fraction by a Fraction

Students will multiply a fraction times a fraction. The students will section off a square through rows and columns that will represent the strategy of multiplying numerators and then denominators.

Professional Development

Name Description
Fractions, Percents, and Ratios, Part A: Models for Multiplication and Division of Fractions

This professional development module shows teachers how to use area models to understand multiplication and division of fractions.

Project

Name Description
Fractions - Cookie Project

This Math Project includes a rubric.
This Math Project includes a permission form.

**** Teacher supplies the hot chocolate for class if you choose to actually do the cookie activity extension.

This activity has two purposes: Math and building a cohesive classroom community. I call these friendship activities and we incorporate activities such as this one into instruction.

Students research from a cookbook, magazine, website, newspaper, etc. a favorite cookie recipe.
Each student copies their recipe on a recipe card (can be an index card).

If you use an index card it can be set up as follows:

Recipe title: _________________ Serves: _______________
Submitted by: ______________________________________
Ingredients:

Procedure:

Research: _________________________________________

The cut the batch to 1/2 and also triple it. This is done on a separate sheet of paper.

Teaching Ideas

Name Description
Why Use the Reciprocal When Dividing Fractions?

Sometimes students ask, "Why are we using the reciprocal when dividing fractions?" This website gives you the language you can use and a visual demonstration of why.

Divide Fractions

This interactive resource provides three activities which model the concept of dividing fractions, as well as mixed numbers, by using number lines or circle graphs.  It includes the equation showing the standard algorithm.

Parent Resources

Teaching Idea

Name Description
Why Use the Reciprocal When Dividing Fractions?:

Sometimes students ask, "Why are we using the reciprocal when dividing fractions?" This website gives you the language you can use and a visual demonstration of why.



Printed On:5/3/2025 11:48:36 PM
Print Page | Close this window