General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
- Solving problems by determining the lengths of the sides in right triangles.
- Finding the measurements of shapes by decomposing complex shapes into simpler ones.
Items may include problems that use the incenter and circumcenter
of a triangle.
Neutral
Students will construct a circle inscribed inside a triangle.
Students will construct a circle circumscribed about a triangle.
Students will solve problems using the properties of inscribed and
circumscribed circles of a triangle.
Students will use or justify properties of angles of a quadrilateral that
is inscribed in a circle.
Item may be set in real-world or mathematical context.
Items may require the student to use or choose the correct unit of
measure.
Items may require the student to provide steps for a construction.
Items may require the student to give statements and/or
justifications to complete formal and informal proofs.
Sample Test Items (1)
| Test Item # | Question | Difficulty | Type |
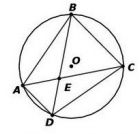
| Sample Item 1 | Trapezoid ABCD is inscribed in circle O. Diagonals
Select the angles and value that make a true statement about trapezoid ABCD. |
N/A | GRID: Graphic Response Item Display |
Related Courses
| Course Number1111 | Course Title222 |
| 1200400: | Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206310: | Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206320: | Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 1206315: | Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current)) |
| 7912065: | Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current)) |
Related Resources
Formative Assessments
| Name | Description |
| Inscribed Quadrilaterals | Students are asked to prove that opposite angles of a quadrilateral, inscribed in a circle, are supplementary. |
| Inscribed Circle Construction | Students are asked to use a compass and straightedge to construct an inscribed circle of an acute scalene triangle. |
| Circumscribed Circle Construction | Students are asked to use a compass and straightedge to construct a circumscribed circle of an acute scalene triangle. |
Lesson Plans
| Name | Description |
| Geometry Problems: Circles and Triangles | This lesson unit is intended to help you assess how well students are able to use geometric properties to solve problems. In particular, the lesson will help you identify and help students who have the following difficulties: The lesson unit will also help students to recognize that there may be different approaches to geometrical problems, and to understand the relative strengths and weaknesses of those approaches. |
| Geometry Problems: Circles and Triangles | This lesson unit is intended to help you assess how well students are able to use geometric properties to solve problems. In particular, the lesson will help you identify and help students who have the following difficulties solving problems by determining the lengths of the sides in right triangles and finding the measurements of shapes by decomposing complex shapes into simpler ones. The lesson unit will also help students to recognize that there may be different approaches to geometrical problems, and to understand the relative strengths and weaknesses of those approaches. |
Original Student Tutorials
| Name | Description |
| Pennant Company Challenge: Inscribed Circles of Triangles | Discover how easy it is for Katie to construct an inscribed circular logo on her company's triangular pennant template. If she completes the task first, she will win a $1000 bonus! Follow along with this interactive tutorial. |
| Good as New | Learn the steps to circumscribe a circle around a triangle in this interactive tutorial about constructions. Grab a compass, straightedge, pencil and paper to follow along! |
Problem-Solving Tasks
| Name | Description |
| Placing a Fire Hydrant | This problem solving task asks students to place a fire hydrant so that it is equal distance from three given points. |
| Locating Warehouse | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Inscribing a triangle in a circle | This problem introduces the circumcenter of a triangle and shows how it can be used to inscribe the triangle in a circle. |
| Circumcenter of a triangle | This task shows that the three perpendicular bisectors of the sides of a triangle all meet in a point, using the characterization of the perpendicular bisector of a line segment as the set of points equidistant from the two ends of the segment. |
| Inscribing a circle in a triangle II | This problem solving task focuses on a remarkable fact which comes out of the construction of the inscribed circle in a triangle: the angle bisectors of the three angles of triangle ABC all meet in a point. |
Virtual Manipulative
| Name | Description |
| Circumscribe a Circle About a Triangle | In this GeoGebraTube interactive worksheet, you can watch the step by step process of circumscribing a circle about a triangle. Using paper and pencil along with this resource will reinforce the concept. |
Worksheet
| Name | Description |
| Inscribing a circle in a triangle I | This problem solving task shows how to inscribe a circle in a triangle using angle bisectors. |
Student Resources
Original Student Tutorials
| Name | Description |
| Pennant Company Challenge: Inscribed Circles of Triangles: | Discover how easy it is for Katie to construct an inscribed circular logo on her company's triangular pennant template. If she completes the task first, she will win a $1000 bonus! Follow along with this interactive tutorial. |
| Good as New: | Learn the steps to circumscribe a circle around a triangle in this interactive tutorial about constructions. Grab a compass, straightedge, pencil and paper to follow along! |
Problem-Solving Tasks
| Name | Description |
| Placing a Fire Hydrant: | This problem solving task asks students to place a fire hydrant so that it is equal distance from three given points. |
| Locating Warehouse: | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Inscribing a triangle in a circle: | This problem introduces the circumcenter of a triangle and shows how it can be used to inscribe the triangle in a circle. |
| Circumcenter of a triangle: | This task shows that the three perpendicular bisectors of the sides of a triangle all meet in a point, using the characterization of the perpendicular bisector of a line segment as the set of points equidistant from the two ends of the segment. |
| Inscribing a circle in a triangle II: | This problem solving task focuses on a remarkable fact which comes out of the construction of the inscribed circle in a triangle: the angle bisectors of the three angles of triangle ABC all meet in a point. |
Virtual Manipulative
| Name | Description |
| Circumscribe a Circle About a Triangle: | In this GeoGebraTube interactive worksheet, you can watch the step by step process of circumscribing a circle about a triangle. Using paper and pencil along with this resource will reinforce the concept. |
Worksheet
| Name | Description |
| Inscribing a circle in a triangle I: | This problem solving task shows how to inscribe a circle in a triangle using angle bisectors. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Placing a Fire Hydrant: | This problem solving task asks students to place a fire hydrant so that it is equal distance from three given points. |
| Locating Warehouse: | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Inscribing a triangle in a circle: | This problem introduces the circumcenter of a triangle and shows how it can be used to inscribe the triangle in a circle. |
| Circumcenter of a triangle: | This task shows that the three perpendicular bisectors of the sides of a triangle all meet in a point, using the characterization of the perpendicular bisector of a line segment as the set of points equidistant from the two ends of the segment. |
| Inscribing a circle in a triangle II: | This problem solving task focuses on a remarkable fact which comes out of the construction of the inscribed circle in a triangle: the angle bisectors of the three angles of triangle ABC all meet in a point. |
Worksheet
| Name | Description |
| Inscribing a circle in a triangle I: | This problem solving task shows how to inscribe a circle in a triangle using angle bisectors. |

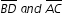 meet at point E and
meet at point E and 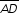 is parallel to
is parallel to 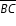 , as shown.
, as shown.