General Information
Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
Test Item Specifications
MAFS.912.G-CO.4.13
Constructions are limited to copying a segment; copying an angle;
bisecting a segment; bisecting an angle; constructing perpendicular
lines, including the perpendicular bisector of a line segment;
constructing a line parallel to a given line through a point not on the
line; constructing an equilateral triangle inscribed in a circle;
constructing a square inscribed in a circle; and a regular hexagon
inscribed in a circle.
Constructions are limited to the use of a formal compass and a
straightedge.
Items should not ask student to find values or use properties of the
geometric figure that is constructed.
Neutral
Students will identify the result of a formal geometric construction.
Students will determine the steps of a formal geometric construction
Items may be set in a real-world or mathematical context.
Items may require the student to justify why a construction results in
the geometric figure.
Items may require the student to use or choose the correct unit of
measure.
Items may require the student to provide steps for a construction.
Sample Test Items (1)
| Test Item # | Question | Difficulty | Type |
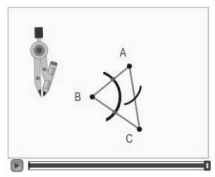
| Sample Item 1 | Ruben carries out a construction using Triangle BC. Click the play button to see a part of his construction,
What will be the result of Ruben's construction? |
N/A | MC: Multiple Choice |
Related Courses
Related Resources
Formative Assessments
| Name | Description |
| Constructing a Congruent Angle | Students are asked to construct an angle congruent to a given angle. |
| Constructions for Parallel Lines | Students are asked to construct a line parallel to a given line through a given point. |
| Constructing a Congruent Segment | Students are asked to construct a line segment congruent to a given line segment. |
| Bisecting a Segment and an Angle | Students are asked to construct the bisectors of a given segment and a given angle and to justify one of the steps in each construction. |
| Constructions for Perpendicular Lines | Students are asked to construct a line perpendicular to given line (1) through a point not on the line and (2) through a point on the line. |
Lesson Plans
| Name | Description |
| Engineering Design Challenge: Exploring Structures in High School Geometry | Students explore ideas on how civil engineers use triangles when constructing bridges. Students will apply knowledge of congruent triangles to build and test their own bridges for stability. |
| Geometric Construction Site | This lesson takes students from simple construction of line segments and angles to an optional extension worksheet for creating triangles. |
| Copying and Bisecting an Angle | This lesson is a gradual release model for constructing congruent angles and bisecting angles. |
| Bisecting Angles And Line Segments | This construction lesson will teach students how to bisect an angle and how to find the perpendicular bisector of a segment using a compass and straightedge. |
| Triangle Medians | This lesson will have students exploring different types of triangles and their medians. Students will construct mid-points and medians to determine that the medians meet at a point. |
| Constructing an Angle Bisector | Students construct an angle bisector given a straightedge and compass then verify their process. The Guided Practice is done in stations. One that is teacher-led and one that is student-led. In order to complete the student-led Guided Practice, access to a teacher computer and projector is needed. Then the students independently create their own angle and its bisector and verify their work for a grade. Students use patty paper and protractors to confirm the accuracy of the construction. |
| Determination of the Optimal Point | Students will use dynamic geometry software to determine the optimal location for a facility under a variety of scenarios. The experiments will suggest a relation between the optimal point and a common concept in geometry; in some cases, there will be a connection to a statistical concept. Algebra can be used to verify some of the conjectures. |
| Back to the Basics: Constructions | Students will use a compass and straightedge to develop methods for constructions. GeoGebra directions are also provided. |
| What's the Point? Part 2 | In this lesson, students use a paper-folding technique to discover the properties of angle bisectors. At the conclusion of the activity, students will be able to compare/contrast the points of concurrency of perpendicular and angle bisectors. |
| Circumnavigating the Circumcenter | Students use the concurrent point of perpendicular bisectors of triangle sides to determine the circumcenter of three points. Students will reason that the circumcenter of the vertices of a polygon is the optimal location for placement of a facility to service all of the needs of sites at the vertices forming the polygon. |
| Crafty Circumference Challenge | Students learn about geometric construction tools and how to use them. Students will partition the circumference of a circle into three, four, and six congruent arcs which determine the vertices of regular polygons inscribed in the circle. An optional project is included where students identify, find, and use recycled, repurposed, or reclaimed objects to create "crafty" construction tools. |
| Right turn, Clyde! | Students will develop their knowledge of perpendicular bisectors & point of concurrency of a triangle, as well as construct perpendicular bisectors through real world problem solving with a map. |
| Halfway to the Middle! | Students will develop their knowledge of mid-segments of a triangle, construct and provide lengths of mid-segments. |
| Location, Location, Location, Location? | Students will use their knowledge of graphing concurrent segments in triangles to locate and identify which points of concurrency are associated by location with cities and counties within the Texas Triangle Mega-region. |
| St. Pi Day construction with a compass & ruler | St. Pi Day construction with compass |
| Determination of the Optimal Point | Students will use dynamic geometry software to determine the optimal location for a facility under a variety of scenarios. The experiments will suggest a relation between the optimal point and a common concept in geometry; in some cases, there will be a connection to a statistical concept. Algebra can be used to verify some of the conjectures. |
| Patterns in Fractals | This lesson is designed to introduce students to the idea of finding patterns in the generation of several different types of fractals. This lesson provides links to discussions and activities related to patterns and fractals as well as suggested ways to work them into the lesson. Finally, the lesson provides links to follow-up lessons designed for use in succession with the current one. |
| What's the Point? Part 1 | This is a patty paper-folding activity where students measure and discover the properties of the point of concurrency of the perpendicular bisectors of the sides of a triangle. |
Original Student Tutorials
| Name | Description |
| Angle UP: Player 1 | Explore the construction processes for constructing an angle bisector, copying an angle and constructing a line parallel to a given line through a point not on the line using a variety of tools in this interactive, retro video game-themed tutorial. NOTE: This tutorial uses both the angle bisector construction and the construction to copy an angle as an extension opportunity to also construct a line parallel to a given line through a point not on the line. Students also learn to identify corresponding angles created when a transversal crosses parallel lines, and discover using Geogebra that these angles are congruent. |
| Meet Me Half Way | Plan a paddle board expedition by learning how to do basic geometric constructions including copying a segment, constructing a segment bisector, constructing a segment's perpendicular bisector and constructing perpendicular segments using a variety of tools in this interactive tutorial. |
| The Blueprints of Construction | Learn to construct the perpendicular bisector of a line segment using a straightedge and compass with this interactive tutorial. |
Presentation/Slideshow
| Name | Description |
| The Pythagorean Theorem: Geometry’s Most Elegant Theorem | This lesson teaches students about the history of the Pythagorean theorem, along with proofs and applications. It is geared toward high school Geometry students that have completed a year of Algebra and addresses the following national standards of the National Council of Teachers of Mathematics and the Mid-continent Research for Education and Learning: 1) Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships; 2) Use visualization, spatial reasoning, and geometric modeling to solve problems; 3) Understand and apply basic and advanced properties of the concepts of geometry; and 4) Use the Pythagorean theorem and its converse and properties of special right triangles to solve mathematical and real-world problems. The video portion is about thirty minutes, and with breaks could be completed in 50 minutes. (You may consider completing over two classes, particularly if you want to allow more time for activities or do some of the enrichment material). These activities could be done individually, in pairs, or groups. I think 2 or 3 students is optimal. The materials required for the activities include scissors, tape, string and markers. |
Problem-Solving Tasks
| Name | Description |
| Inscribing a square in a circle | This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context. |
| Construction of perpendicular bisector | This problem solving task challenges students to construct a perpendicular bisector of a given segment. |
| Reflected Triangles | This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected. |
| Bisecting an angle | This problem solving task challenges students to bisect a given angle. |
| Locating Warehouse | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Angle bisection and midpoints of line segments | This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts. |
Unit/Lesson Sequence
| Name | Description |
| Three Dimensional Shapes | In this interactive, self-guided unit on 3-dimensional shape, students (and teachers) explore 3-dimensional shapes, determine surface area and volume, derive Euler's formula, and investigate Platonic solids. Interactive quizzes and animations are included throughout, including a 15 question quiz for student completion. |
Video/Audio/Animation
| Name | Description |
| MIT BLOSSOMS - Using Geometry to Design Simple Machines | This video is meant to be a fun, hands-on session that gets students to think hard about how machines work. It teaches them the connection between the geometry that they study and the kinematics that engineers use -- explaining that kinematics is simply geometry in motion. |
Student Resources
Original Student Tutorials
| Name | Description |
| Angle UP: Player 1: | Explore the construction processes for constructing an angle bisector, copying an angle and constructing a line parallel to a given line through a point not on the line using a variety of tools in this interactive, retro video game-themed tutorial. NOTE: This tutorial uses both the angle bisector construction and the construction to copy an angle as an extension opportunity to also construct a line parallel to a given line through a point not on the line. Students also learn to identify corresponding angles created when a transversal crosses parallel lines, and discover using Geogebra that these angles are congruent. |
| Meet Me Half Way: | Plan a paddle board expedition by learning how to do basic geometric constructions including copying a segment, constructing a segment bisector, constructing a segment's perpendicular bisector and constructing perpendicular segments using a variety of tools in this interactive tutorial. |
| The Blueprints of Construction: | Learn to construct the perpendicular bisector of a line segment using a straightedge and compass with this interactive tutorial. |
Presentation/Slideshow
| Name | Description |
| The Pythagorean Theorem: Geometry’s Most Elegant Theorem: | This lesson teaches students about the history of the Pythagorean theorem, along with proofs and applications. It is geared toward high school Geometry students that have completed a year of Algebra and addresses the following national standards of the National Council of Teachers of Mathematics and the Mid-continent Research for Education and Learning: 1) Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop mathematical arguments about geometric relationships; 2) Use visualization, spatial reasoning, and geometric modeling to solve problems; 3) Understand and apply basic and advanced properties of the concepts of geometry; and 4) Use the Pythagorean theorem and its converse and properties of special right triangles to solve mathematical and real-world problems. The video portion is about thirty minutes, and with breaks could be completed in 50 minutes. (You may consider completing over two classes, particularly if you want to allow more time for activities or do some of the enrichment material). These activities could be done individually, in pairs, or groups. I think 2 or 3 students is optimal. The materials required for the activities include scissors, tape, string and markers. |
Problem-Solving Tasks
| Name | Description |
| Inscribing a square in a circle: | This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context. |
| Construction of perpendicular bisector: | This problem solving task challenges students to construct a perpendicular bisector of a given segment. |
| Reflected Triangles: | This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected. |
| Bisecting an angle: | This problem solving task challenges students to bisect a given angle. |
| Locating Warehouse: | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Angle bisection and midpoints of line segments: | This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts. |
Parent Resources
Problem-Solving Tasks
| Name | Description |
| Inscribing a square in a circle: | This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context. |
| Construction of perpendicular bisector: | This problem solving task challenges students to construct a perpendicular bisector of a given segment. |
| Reflected Triangles: | This task asks students to use a straightedge and compass to construct the line across which a triangle is reflected. |
| Bisecting an angle: | This problem solving task challenges students to bisect a given angle. |
| Locating Warehouse: | This problem solving task challenges students to place a warehouse (point) an equal distance from three roads (lines). |
| Angle bisection and midpoints of line segments: | This task provides a construction of the angle bisector of an angle by reducing it to the bisection of an angle to finding the midpoint of a line segment. It is worth observing the symmetry -- for both finding midpoints and bisecting angles, the goal is to cut an object into two equal parts. |