For exponential models, express as a logarithm the solution to
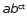
= d where a, c, and d are numbers and the base b is 2, 10, or e;
evaluate the logarithm using technology.
★
| Name |
Description |
| Algae Blooms | In this example, students are asked to write a function describing the population growth of algae. It is implied that this is exponential growth. |
| Snail Invasion | The purpose of this task is to give students experience modeling a real-world example of exponential growth, in a context that provides a vivid illustration of the power of exponential growth, for example the cost of inaction for a year. There is an opportunity for further discussion based on part (c), since the ratio of costs from one year to the next is the same in each part. |
| Newton's Law of Cooling | The coffee cooling experiment is a popular example of an exponential model with immediate appeal. The model is realistic and provides a good context for students to practice work with exponential equations. |
| Carbon 14 Dating in Practice II | This problem introduces the method used by scientists to date certain organic material. It is based not on the amount of the Carbon 14 isotope remaining in the sample but rather on the ratio of Carbon 14 to Carbon 12. This ratio decreases, hypothetically, at a constant exponential rate as soon as the organic material has ceased to absorb Carbon 14, that is, as soon as it dies. |
| Carbon 14 Dating | The task requires the student to use logarithms to solve an exponential equation in the realistic context of carbon dating, important in archaeology and geology, among other places. Students should be guided to recognize the use of the natural logarithm when the exponential function has the given base of e, as in this problem. Note that the purpose of this task is algebraic in nature -- closely related tasks exist which approach similar problems from numerical or graphical stances. |
| Bacteria Populations | This task provides a real world context for interpreting and solving exponential equations. There are two solutions provided for part (a). The first solution demonstrates how to deduce the conclusion by thinking in terms of the functions and their rates of change. The second approach illustrates a rigorous algebraic demonstration that the two populations can never be equal. |
| Name |
Description |
| Algae Blooms: | In this example, students are asked to write a function describing the population growth of algae. It is implied that this is exponential growth. |
| Snail Invasion: | The purpose of this task is to give students experience modeling a real-world example of exponential growth, in a context that provides a vivid illustration of the power of exponential growth, for example the cost of inaction for a year. There is an opportunity for further discussion based on part (c), since the ratio of costs from one year to the next is the same in each part. |
| Newton's Law of Cooling: | The coffee cooling experiment is a popular example of an exponential model with immediate appeal. The model is realistic and provides a good context for students to practice work with exponential equations. |
| Carbon 14 Dating in Practice II: | This problem introduces the method used by scientists to date certain organic material. It is based not on the amount of the Carbon 14 isotope remaining in the sample but rather on the ratio of Carbon 14 to Carbon 12. This ratio decreases, hypothetically, at a constant exponential rate as soon as the organic material has ceased to absorb Carbon 14, that is, as soon as it dies. |
| Carbon 14 Dating: | The task requires the student to use logarithms to solve an exponential equation in the realistic context of carbon dating, important in archaeology and geology, among other places. Students should be guided to recognize the use of the natural logarithm when the exponential function has the given base of e, as in this problem. Note that the purpose of this task is algebraic in nature -- closely related tasks exist which approach similar problems from numerical or graphical stances. |
| Bacteria Populations: | This task provides a real world context for interpreting and solving exponential equations. There are two solutions provided for part (a). The first solution demonstrates how to deduce the conclusion by thinking in terms of the functions and their rates of change. The second approach illustrates a rigorous algebraic demonstration that the two populations can never be equal. |
| Name |
Description |
| Algae Blooms: | In this example, students are asked to write a function describing the population growth of algae. It is implied that this is exponential growth. |
| Snail Invasion: | The purpose of this task is to give students experience modeling a real-world example of exponential growth, in a context that provides a vivid illustration of the power of exponential growth, for example the cost of inaction for a year. There is an opportunity for further discussion based on part (c), since the ratio of costs from one year to the next is the same in each part. |
| Newton's Law of Cooling: | The coffee cooling experiment is a popular example of an exponential model with immediate appeal. The model is realistic and provides a good context for students to practice work with exponential equations. |
| Carbon 14 Dating in Practice II: | This problem introduces the method used by scientists to date certain organic material. It is based not on the amount of the Carbon 14 isotope remaining in the sample but rather on the ratio of Carbon 14 to Carbon 12. This ratio decreases, hypothetically, at a constant exponential rate as soon as the organic material has ceased to absorb Carbon 14, that is, as soon as it dies. |
| Carbon 14 Dating: | The task requires the student to use logarithms to solve an exponential equation in the realistic context of carbon dating, important in archaeology and geology, among other places. Students should be guided to recognize the use of the natural logarithm when the exponential function has the given base of e, as in this problem. Note that the purpose of this task is algebraic in nature -- closely related tasks exist which approach similar problems from numerical or graphical stances. |
| Bacteria Populations: | This task provides a real world context for interpreting and solving exponential equations. There are two solutions provided for part (a). The first solution demonstrates how to deduce the conclusion by thinking in terms of the functions and their rates of change. The second approach illustrates a rigorous algebraic demonstration that the two populations can never be equal. |

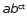 = d where a, c, and d are numbers and the base b is 2, 10, or e;
evaluate the logarithm using technology.
= d where a, c, and d are numbers and the base b is 2, 10, or e;
evaluate the logarithm using technology.