General Information
Subject Area: X-Mathematics (former standards - 2008)
Grade: 912
Body of Knowledge: Algebra
Standard: Logarithmic and Exponential Functions - Understand the concepts of logarithmic and exponential functions. Graph exponential functions, and solve problems of growth and decay. Understand the inverse relationship between exponents and logarithms, and use it to prove laws of logarithms and to solve equations. Convert logarithms between bases, and simplify logarithmic expressions.
Date Adopted or Revised: 09/07
Content Complexity Rating:
Level 3: Strategic Thinking & Complex Reasoning
-
More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived

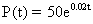 , where P(t) is the population in millions and t is the number of years after 1900. Find when the population is 100 million, 200 million, and 400 million. What do you notice about these time periods?
, where P(t) is the population in millions and t is the number of years after 1900. Find when the population is 100 million, 200 million, and 400 million. What do you notice about these time periods?