Standard #: MA.912.A.3.9 (Archived Standard)


This document was generated on CPALMS - www.cpalms.org



Determine the slope, x-intercept, and y-intercept of a line given its graph, its equation, or two points on the line.


Remarks


Example: Find the slope and y-intercept of the line described by the equation 4x + 6y = 9.

General Information

Subject Area: X-Mathematics (former standards - 2008)
Grade: 912
Body of Knowledge: Algebra
Standard: Linear Equations and Inequalities - Solve linear equations and inequalities.
Date Adopted or Revised: 09/07
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived
Assessed: Yes

Test Item Specifications

    Item Type(s): This benchmark may be assessed using: MC , FR item(s)
    Also Assesses:

    MA.912.A.3.12 Graph a linear equation or inequality in two variables with and without graphing technology. Write an equation or inequality represented by a given graph.

    Clarification :
    Students will determine the slope, x-intercept, and/or y-intercept of a line given its graph, its equation, or two points on the line.
    Content Limits :
    Items may include lines that have zero slope or undefined slope.
    Stimulus Attributes :

    Items may be set in either real-world or mathematical contexts.

    Items may include linear equations in various forms, including standard, slope-intercept, and point-slope forms.

    Graphics should be used in most of these items, as appropriate.

    Response Attributes :

    Fill-in response items may require that students provide a slope or the x-coordinate (or y-coordinate) of a point of interest.

    Fill-in response items may have a negative answer.



Sample Test Items (2)

Test Item # Question Difficulty Type
Sample Item 1 An architect designed an outdoor staircase for a house. The relationship between the height of the steps and the length of the tread is modeled by the equation 57x - 95y = 0.
Which of the following represents the slope of the equation?		 N/A MC: Multiple Choice
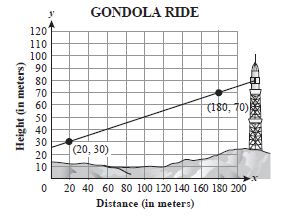
Sample Item 2

An engineer needs to determine the slope between two points on a gondola ride in order to evaluate the power requirements when the gondola is full of passengers. A coordinate grid has been placed over a diagram between the two points, as shown below. For estimation purposes, a straight line between the two points can be used to find the slope.

 

Assuming the cable runs in a straight line, what is the slope of the line between the two points shown?

 N/A FR: Fill-in Response


Related Resources

Unit/Lesson Sequence

Name Description
Direct and Inverse Variation "Lesson 1 of two lessons teaches students about direct variation by allowing them to explore a simulated oil spill using toilet paper tissues (to represent land) and drops of vegetable oil (to simulate a volume of oil). Lesson 2 teaches students about inverse variation by exploring the relationship between the heights of a fixed amount of water poured into cylindrical containers of different sizes as compared to the area of the containers' bases." from Insights into Algebra 1 - Annenberg Foundation.
Printed On:5/2/2025 6:22:10 AM
Print Page | Close this window