Standard #: MA.912.G.3.3 (Archived Standard)


This document was generated on CPALMS - www.cpalms.org



Use coordinate geometry to prove properties of congruent, regular, and similar quadrilaterals.


Remarks


Coordinate geometry is used while students prove quadrilaterals to be congruent, similar, or regular.

Coordinate geometry is used to prove properties of quadrilaterals.

Example: Given a quadrilateral with vertices (0, 0), (5/2, 5sqrt(3)/2), (5, 0), (7, 7sqrt(3)/3), prove that the diagonals of this quadrilateral are perpendicular.

Example: Is rectangle ABCD with vertices at A(0, 0), B(4, 0), C(4, 2), D(0, 2) congruent to rectangle PQRS with vertices at P(-2, -1), Q(2, -1), R(2, 1), S(-2, 1)? Justify your answer.



General Information

Subject Area: X-Mathematics (former standards - 2008)
Grade: 912
Body of Knowledge: Geometry
Idea: Level 3: Strategic Thinking & Complex Reasoning
Standard: Quadrilaterals - Classify and understand relationships among quadrilaterals (rectangle, parallelogram, kite, etc.). Relate geometry to algebra by using coordinate geometry to determine regularity, congruence, and similarity. Use properties of congruent and similar quadrilaterals to solve problems involving lengths and areas, and prove theorems involving quadrilaterals.
Date Adopted or Revised: 09/07
Content Complexity Rating: Level 3: Strategic Thinking & Complex Reasoning - More Information
Date of Last Rating: 06/07
Status: State Board Approved - Archived
Assessed: Yes

Test Item Specifications

    Item Type(s): This benchmark may be assessed using: MC item(s)
    N/A

    Clarification :
    Students will use coordinate geometry and geometric properties to justify measures and characteristics of congruent, regular, and similar quadrilaterals.
    Content Limits :

    Items may include statements and/or justifications to complete formal and informal proofs.

     Items may include the use of coordinate planes.

    Stimulus Attributes :

    Graphics should be used for most of these items, as appropriate.

    Items may be set in either real-world or mathematical contexts.



Sample Test Items (1)

Test Item # Question Difficulty Type
Sample Item 1

On the coordinate grid below, quadrilateral ABCD has vertices with integer coordinates.

 

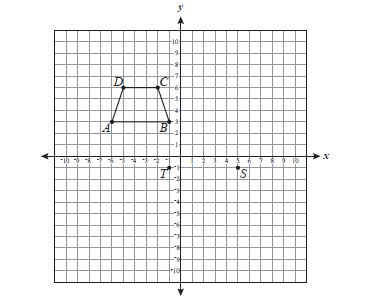Quadrilateral QRST is similar to quadrilateral ABCD with point S located at (5, -1) and point T located at (-1, -1). Which of the following could be possible coordinates for point Q?

 N/A MC: Multiple Choice


Printed On:5/4/2025 11:55:46 AM
Print Page | Close this window