General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Coordinate Plane
- Dilation
- Origin
- Reflection
- Rigid Transformation
- Rotation
- Scale Factor
- Translation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students first learned to associate congruence and similarity with reflections, rotations, translations and dilations. In Geometry, students learn that these transformations provide an equivalent alternative to using congruence and similarity criteria for triangles.- Instruction includes the connection to the Angle-Angle, Side-Angle-Side, Hypotenuse-Leg and Side-Side-Side similarity criteria and to justifying congruence criteria.
- For example, if one wants to justify the Angle-Angle criterion, one method is as follows: Start with triangles ABC and PQR, with ∠A ≅ ∠P and ∠B ≅ ∠Q, as shown below.Students should be able to realize the need of a dilation, in this case with a scale factor such that 0 < < 1 and = . After this dilation, triangle A’B’C’ is obtained, such that the length of A’B’ equals the length of PQ. Since dilations preserve angle measures, ∠A ≅ ∠A′ and ∠B ≅ ∠B′. Using the transitive property of congruence, if ∠A ≅ ∠P and ∠A ≅ ∠A′, then ∠P ≅ ∠A′, and if ∠B ≅ ∠Q and ∠B ≅ ∠B′, then ∠Q ≅ ∠B′. With PQ ≅ A′B′, ∠P ≅ ∠A′ and ∠Q ≅ ∠B′, we can prove ΔPQR ≅ ΔA′B′C′ by Side-Angle-Side Congruence Criterion. Additionally, since ΔABC~ΔA′B′C′ and ΔPQR ≅ ΔA′B′C′, it can be concluded that ΔABC~ΔPQR. Justification of the other criteria can be done in a similar manner.
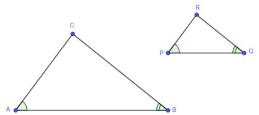
- For example, if one wants to justify the Angle-Angle criterion, one method is as follows: Start with triangles ABC and PQR, with ∠A ≅ ∠P and ∠B ≅ ∠Q, as shown below.
Common Misconceptions or Errors
- When determining the scale factor of a dilation, students may misidentify the preimage and image, leading to an incorrect scale factor.
Instructional Tasks
Instructional Task 1 (MTR.3.1, MTR.4.1)- Triangle XYZ has the coordinates (0,2), (2,4) and (6,0) and triangle DEF has the coordinates (4, −4), (8,0) and (16, −8).
- Part A. How can ΔACB~ΔLMN be proved using one of the similarity criteria?
- Part B. How can ΔACB~ΔLMN be proved using rigid and non-rigid transformations?
Instructional Items
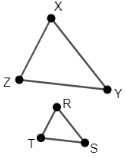
Instructional Item 1- Shown below are two triangles where ∠X = ∠R, ∠Y = ∠S, and ∠Z = ∠T. Determine a dilation that maps ΔXYZ onto ΔRST.
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
