General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students used organized lists, tables and tree diagrams to determine sample spaces for repeated experiments. In Algebra I, students considered combinations of solutions in reference to two-variable inequalities and constraints on systems of equations and inequalities. Algebra I Honors extended the grade 8 strategies for determining sample spaces to help organize information when constructing relative frequency tables. In Math for College Liberal Arts, students consider new ways to organize data when calculating permutations and combinations.- Instruction includes explorations of real-world situations requiring counting. Begin with an example where students are able to easily write out all of the possible combinations and count, or use visual representations such as a tree diagram (MTR.2.1). Then move toward examples where counting becomes more cumbersome or time-consuming, generating an interest to find a more efficient method to calculate.
- Instruction introduces the concept of Fundamental Counting Principle. This includes the idea that if you can choose one item from a group of M items and a second item from a group of N items, then the total number of two-item choices is M × N. In other words, the number of ways in which a series of successive things can occur is found by multiplying the number of ways in which each thing can occur.
- Depending on a student’s pathway, this may be the first time students interact with factorials. Begin with an example that will allow students to make sense of this concept. n factorial is the product of all the positive integers less than or equal to a non-negative
integer, n. This is represented by n!.
- For example, at graduation, the valedictorian, salutatorian, and student council president will all stand on stage until it is time to hand out diplomas. How many possible seating arrangements will accommodate this honor?
- Connect students’ visual representations and counts to 3!.
- A students’ visual representation could show the following:
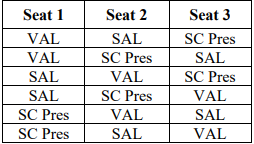
- A students’ visual representation could show the following:
- Students could also represent the situation as 3!. This means that Seat 1 has 3 choices, Seat 2 then has 2 choices, and Seat 3 has 1 choice. Students can show that 3! is equivalent to 3 × 2 × 1, representing the 6 possible seating arrangements described in the table above.
- Instruction includes open-ended questions where students must decide for themselves if
order matters or if repetition is acceptable (MTR.4.1). This allows exploration of both
permutations and combinations.
- For example, in a group of 7 students, 3 will win an award for most participation. Students can then discuss if they believe this should be given as 1st, 2nd or 3rd place, or if 3 students are chosen and given the same award. Have students explore different options, explain their reasoning and work toward developing appropriate “rules” for the different scenarios.
- As students explore the concepts, instruction includes naming a permutation as an
arrangement of a subset of a particular size (r) taken from a set of a certain size (n), with
regard to the order of the arrangement, while a combination is a selection of a subset of a
particular size (r) taken from a set of a certain size (n), without regard to the
order/arrangement of the selection. Students should explore these concepts by showing
the different permutations and combinations and see how the number of arrangements
and groupings compare.
- For example, when arranging the letters A, B and C, ABC is a different permutation than BCA. However, ABC is considered the same combination as BCA.
- Instruction includes various representations/symbols for calculating permutations and
combinations. Once formulas are established, use mathematical context to ensure
students can accurately use technology in these calculations.
- nPr = P(n, r) = where n is the number of objects in a set and r is the
number of objects in the subset being chosen.
- For example, a coach must choose a batting order of 9 players. He has 18 players to choose from. How many batting orders are possible?
- nCr = C(n, r) = (nr) =
where n is the number of objects in a set and r is
the number of objects in the subset being chosen.
- For example, a coach must choose a team of 9 players. He has 18 players to choose from. How many teams are possible?
- nPr = P(n, r) = where n is the number of objects in a set and r is the
number of objects in the subset being chosen.
Common Misconceptions or Errors
- Students may double count arrangements when creating displays or working outside of the formulas for permutations and combinations.
- Students may confuse when a problem is asking for a permutation or a combination. To address this misconception, emphasize that order matters for a permutation but not a combination.
- Students may not use factorials correctly.
- Students may add, rather than multiply, when calculating the number of possible arrangements. To address this misconception, provide a scenario where students can easily write out all possible arrangements, count, and compare to their original
Instructional Tasks
Instructional Task 1- There are 18 students on the Fierce Felines swim team.
- Part A. If all 18 students compete in a practice swim prior to the official start of a meet, how many outcomes for the Fierce Felines are there?
- Part B. The coach needs to choose 4 students for the freestyle relay event. How many different ways can the coach choose students for this event?
- Part C. Eight swimmers from four schools are competing in the 100 individual medley. How many ways can 1st, 2nd, and 3rd place occur for this event?
- Part A. Using a real-world context, write a scenario requiring the use of the combination formula and calculate its answer. What criteria in your scenario shows that this is a combination?
- Part B. Using a real-world context, write a scenario requiring the use of the permutation formula and calculate its answer. What criteria in your scenario shows that this is a permutation?
- Part C. Exchange your scenarios with a partner and calculate the answers. Did your answers match?
Instructional Items
Instructional Item 1- There are 7 seniors this year on the soccer team, but only two can be named co-captains for the season. How many ways can the co-captains be assigned by the coach?
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
