General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Inscribed Polygon in a Circle
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 8, students learned about regular polygons and their interior angles. In Geometry, students inscribe such polygons in circles using compass and straightedge.- Instruction includes the use of manipulatives, tools and geometric software. Allowing students to explore constructions with dynamic software reinforces why the constructions work.
- Instruction includes the student understanding that in a geometric construction, one does not use the markings on a ruler or on a protractor to construct inscribed and circumscribed circles of a triangle. Students should realize that there are limitations on precision that are inherent in the markings on rulers or protractors.
- It is important to build the understanding that formal constructions are valid when the lengths of segments or measures of angles are not known, or have values that do not appear on a ruler or protractor, including irrational values.
- Instruction includes the connection to logical reasoning and visual proofs when verifying that a construction works.
- To construct a square inscribed in a circle given the center of the circle, the procedure can start by drawing one of the diameters of the circle. This diameter will be one of the diagonals of the square. Then, students can construct the perpendicular bisector of the drawn diameter. The perpendicular bisector will intersect the circle in two points resulting in another diameter of the circle that is congruent and perpendicular to the drawn diameter. Students should realize that diagonals of squares have the same length and are perpendicular bisectors of one another. Therefore, the two diameters are the diagonals of the square to be constructed in the circle. To construct this square, draw the sides by connecting each of the endpoints of the diagonals.
- The construction of a regular hexagon inscribed in a circle (given the center) can start by choosing one point, P on the circle, then, with the compass setting equal to the radius of the circle, students can draw an arc intersecting the circle at the point Q. Students should realize that the two points on the circle and the center of the circle are the vertices of an equilateral triangle. Students can then move the compass to the point Q and draw another arc intersecting the circle at the point R. Students can repeat this process as they move around the circle until the arrive back at the point P. Students should realize that as they are repeating this process around the circle, they are forming six equilateral triangles. These triangles compose the regular hexagon that is inscribed in the circle.
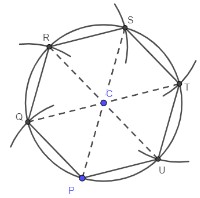
- The construction of an equilateral triangle can begin by constructing a regular hexagon, as described above. Once the six equilateral triangles have been formed, to construct an equilateral triangle in the circle, students can join three pairs of alternating vertices (as shown below).
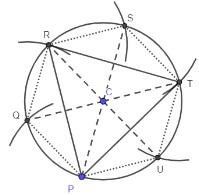
- Instruction includes the connection to the sum of the measures of the interior angles of a regular polygon to the construction of equilateral triangles and hexagons inscribed in a circle.
- Enrichment of this benchmark includes constructing other regular polygons, such as octagons and dodecagons, using angle bisection.
- For expectations of this benchmark, constructions should be reasonably accurate and the emphasis is to make connections between the construction steps and the definitions, properties and theorems supporting them.
- While going over the steps of geometric constructions, ensure that students develop vocabulary to describe the steps precisely. (MTR.4.1)
- Problem types include identifying the next step of a construction, a missing step in a construction or the order of the steps in a construction.
Common Misconceptions or Errors
- Students may think or determine that when constructing a regular hexagon, they will not have all equal side lengths. To help address this, reiterate the importance of precision and accuracy when using a compass.
Instructional Tasks
Instructional Task 1- Circle A is provided below.
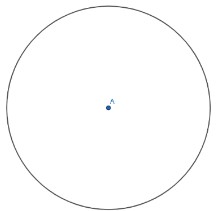
- Part A. What do you know about all the points on circle A in relation to point A?
- Part B. Draw a point J on circle A. Open the compass to the length of the resulting radius of circle A.
- Part C. With the compass point on point J, arc on both sides of J making sure to intersect circle A. Label the points of intersection as J and M.
- Part D. Classify triangle AKJ by sides.
- Part E. What is the measure of angle KJM?
- Part F. What is the measure of an interior angle of a regular hexagon?
- Part G. What process could be used to continue constructing a regular hexagon that is inscribed in circle A?
- Part H. How could the construction of an inscribed regular hexagon be used to construct an inscribed equilateral triangle?
Instructional Task 2 (MTR.3.1, MTR.4.1, MTR.5.1)
- Part A. Construct a regular hexagon inscribed in a circle.
- Part B. Prove that the constructed hexagon is a regular hexagon.
- Part C. Prove that if three pairs of alternating vertices of the hexagon from Part A are joined, it creates an equilateral triangle.
- Part D. Compare your proof from Part C with a partner.
Instructional Items
Instructional Item 1- Describe the steps to construct a square inscribed in circle J.
