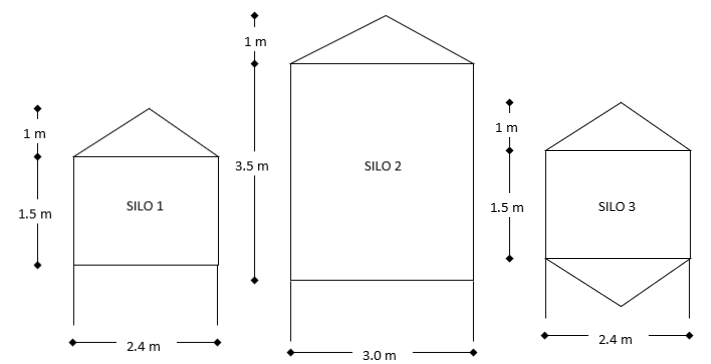
Solve mathematical and real-world problems involving the volume of three-dimensional figures limited to cylinders, pyramids, prisms, cones and spheres.
: A cylindrical swimming pool is filled with water and has a diameter of 10 feet and height of 4 feet. If water weighs 62.4 pounds per cubic foot, what is the total weight of the water in a full tank to the nearest pound?
Instruction includes concepts of density based on volume.
| Name |
Description |
| Volume of a Cylinder | Students are asked to derive and explain a formula for the volume of a cylinder given a prism with the same height and the same cross-sectional area at every height. |
| Estimating Volume | Students are asked to model a tree trunk with geometric solids and to use the model to estimate the volume of the tree trunk. |
| Volume of a Cone | Students are asked to derive and explain a formula for the volume of a cone given a pyramid with the same height and the same cross-sectional area at every height. |
| Mudslide | Students are asked to create a model to estimate volume and mass. |
| Volume of a Pyramid | Students are guided through the process of writing an informal argument for the volume of a pyramid formula using Cavalieri’s Principle. |
| Sugar Cone | Students are asked to solve a problem that requires calculating the volume of a cone. |
| Louvre Pyramid | Students are asked to find the height of a square pyramid given the length of a base edge and its volume. |
| Cylinder Formula | Students are asked to write the formula for the volume of a cylinder, explain what each variable represents, and label the variables on a diagram. |
| Cone Formula | Students are asked to write the formula for the volume of a cone, explain what each variable represents, and label the variables on a diagram. |
| Burning Sphere | Students are asked to solve a problem that requires calculating the volume of a sphere. |
| Chilling Volumes | Students are asked to solve a problem involving the volume of a composite figure. |
| Sphere Formula | Students are asked to write the formula for the volume of a sphere, explain what each variable represents, and label the variables on a diagram. |
| Pyramid Formula | Students are asked to write the formula for the volume of a pyramid, explain what each variable represents, and label the variables on a diagram. |
| Snow Cones | Students are asked to solve a problem that requires calculating the volumes of a cone and a cylinder. |
| Sports Drinks | Students are asked to solve a problem that requires calculating the volume of a large cylindrical sports drink container and comparing it to the combined volumes of 24 individual containers. |
| The Great Pyramid | Students are asked to find the height of the Great Pyramid of Giza given its volume and the length of the edge of its square base. |
| Do Not Spill the Water! | Students are asked to solve a problem that requires calculating the volumes of a sphere and a cylinder. |
| Name |
Description |
| How Many Cones Does It Take? | This lesson is a "hands-on" activity. Students will investigate and compare the volumes of cylinders and cones with matching radii and heights. Students will first discover the relationship between the volume of cones and cylinders and then transition into using a formula to determine the volume. |
| Filled to Capacity! | This is a lesson where students investigate, compare, dissect, and use the relationship between volume of a cone and cylinder with equal corresponding dimensions. |
| The Relationship Between Cones and Cylinders | Students create a cone and a cylinder with the same height and base. At the conclusion of the lesson, the students will know that the volume ratio between the cone and cylinder is 1:3. |
| Exploring Cavalieri's Principle | Students will explore Cavalieri's Principle using technology. Students will calculate the volume of oblique solids and determine if Cavalieri's Principle applies.
Students will also perform transformations of a base figure in a 3-dimensional coordinate system to observe the creation of right and oblique solid figures. After these observations, students will create a conjecture about calculating the volume of the oblique solids. Students will use the conjecture to determine situations in which Cavalieri's Principle applies and then calculate the volume of various oblique solids. |
| Find your Formula! | Students will investigate the formula for the volume of a pyramid and/or cone and use those formulas to calculate the volume of other solids. The students will have hands-on discovery working with hollow Geometric Solids that they fill with dry rice, popcorn, or another material. |
| Cape Florida Lighthouse: Lore and Calculations | The historic Cape Florida Lighthouse, often described as a conical tower, teems with mathematical applications. This lesson focuses on the change in volume and lateral surface area throughout its storied existence. |
| Yogurt Land Container | The student will assist Yogurt Land on choosing a new size container to offer their customers. The choice of containers are different three dimensional figures. Students will revisit the concepts of volume, surface area, and profit in order to make a decision.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Propensity for Density | Students apply concepts of density to situations that involve area (2-D) and volume (3-D). |
| Area to Volume Exploration | In this student-centered lesson, the formulas for the volume of a cylinder, cone, and a sphere are examined and practiced. The relationship between the volume of a cone and a cylinder with the same radius and height is explored. Students will also solve real-world problems involving these three-dimensional figures. |
| Pack It Up | Students use geometry formulas to solve a fruit growing company's dilemma of packing fruit into crates of varying dimensions. Students calculate the volume of the crates and the volume of the given fruit when given certain numerical facts about the fruit and the crates. Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Volumes about Volume | This lesson explores the formulas for calculating the volume of cylinders, cones, pyramids, and spheres. |
| The Cost of Keeping Cool | Students will find the volumes of objects. After decomposing a model of a house into basic objects students will determine the cost of running the air conditioning. |
| Which Brand of Chocolate Chip Cookie Would You Buy? | In this activity, students will utilize measurement data provided in a chart to calculate areas, volumes, and densities of cookies. They will then analyze their data and determine how these values can be used to market a fictitious brand of chocolate chip cookie. Finally, they will integrate cost and taste into their analyses and generate a marketing campaign for a cookie brand of their choosing based upon a set sample data which has been provided to them.
Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. Click here to learn more about MEAs and how they can transform your classroom. |
| Victorious with Volume | In this lesson, the students will explore and use the relationship of volume for cylinders and cones that have equal heights and radii. |
| M&M Soup | This is the informative part of a two-lesson sequence. Students explore how to find the volume of a cylinder by making connections with circles and various real-world items. |
| Calculating Volumes of Compound Objects | This lesson unit is intended to help you assess how well students solve problems involving measurement, and in particular, to identify and help students who have the following difficulties:
- Computing measurements using formulas.
- Decomposing compound shapes into simpler ones.
- Using right triangles and their properties to solve real-world problems.
|
| Name |
Description |
| How thick is a soda can? (Variation II) | This problem solving task asks students to explain which measurements are needed to estimate the thickness of a soda can. Multiple solution processes are presented. |
| Archimedes and the King's Crown | This problem solving task uses the tale of Archimedes and the King of Syracuse's crown to determine the volume and mass of gold and silver. |
| Doctor's Appointment | The purpose of the task is to analyze a plausible real-life scenario using a geometric model. The task requires knowledge of volume formulas for cylinders and cones, some geometric reasoning involving similar triangles, and pays attention to reasonable approximations and maintaining reasonable levels of accuracy throughout. |
| Centerpiece | The purpose of this task is to use geometric and algebraic reasoning to model a real-life scenario. In particular, students are in several places (implicitly or explicitly) to reason as to when making approximations is reasonable and when to round, when to use equalities vs. inequalities, and the choice of units to work with (e.g., mm vs. cm). |
| Use Cavalieri’s Principle to Compare Aquarium Volumes | This task presents a context that leads students toward discovery of the formula for calculating the volume of a sphere. |
| Tennis Balls in a Can | This task is inspired by the derivation of the volume formula for the sphere. If a sphere of radius 1 is enclosed in a cylinder of radius 1 and height 2, then the volume not occupied by the sphere is equal to the volume of a "double-naped cone" with vertex at the center of the sphere and bases equal to the bases of the cylinder |
| Glasses | In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem. |
| Comparing Snow Cones | Students will just be learning about similarity in this grade, so they may not recognize that it is needed in this context. Teachers should be prepared to give support to students who are struggling with this part of the task. To simplify the task, the teacher can just tell the students that based on the slant of the truncated conical cup, the complete cone would be 14 in tall and the part that was sliced off was 10 inches tall. (See solution for an explanation.) There is a worthwhile discussion to be had about parts (c) and (e). The percentage increase is smaller for the snow cones than it was for the juice treats. The snow cones have volume which is equal to those of the juice treats plus the volume of the dome, which is the same in both cases. Adding the same number to two numbers in a ratio will always make their ratio closer to one, which in this case means that the ratio - and thus percentage increase - would be smaller. |
| Flower Vases | The purpose of this task is to give students practice working the formulas for the volume of cylinders, cones and spheres, in an engaging context that provides and opportunity to attach meaning to the answers. |
| Shipping Rolled Oats | Students should think of different ways the cylindrical containers can be set up in a rectangular box. Through the process, students should realize that although some setups may seem different, they result in a box with the same volume. In addition, students should come to the realization (through discussion and/or questioning) that the thickness of a cardboard box is very thin and will have a negligible effect on the calculations. |
| Name |
Description |
| How thick is a soda can? (Variation II): | This problem solving task asks students to explain which measurements are needed to estimate the thickness of a soda can. Multiple solution processes are presented. |
| Archimedes and the King's Crown: | This problem solving task uses the tale of Archimedes and the King of Syracuse's crown to determine the volume and mass of gold and silver. |
| Doctor's Appointment: | The purpose of the task is to analyze a plausible real-life scenario using a geometric model. The task requires knowledge of volume formulas for cylinders and cones, some geometric reasoning involving similar triangles, and pays attention to reasonable approximations and maintaining reasonable levels of accuracy throughout. |
| Centerpiece: | The purpose of this task is to use geometric and algebraic reasoning to model a real-life scenario. In particular, students are in several places (implicitly or explicitly) to reason as to when making approximations is reasonable and when to round, when to use equalities vs. inequalities, and the choice of units to work with (e.g., mm vs. cm). |
| Use Cavalieri’s Principle to Compare Aquarium Volumes: | This task presents a context that leads students toward discovery of the formula for calculating the volume of a sphere. |
| Tennis Balls in a Can: | This task is inspired by the derivation of the volume formula for the sphere. If a sphere of radius 1 is enclosed in a cylinder of radius 1 and height 2, then the volume not occupied by the sphere is equal to the volume of a "double-naped cone" with vertex at the center of the sphere and bases equal to the bases of the cylinder |
| Glasses: | In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem. |
| Comparing Snow Cones: | Students will just be learning about similarity in this grade, so they may not recognize that it is needed in this context. Teachers should be prepared to give support to students who are struggling with this part of the task. To simplify the task, the teacher can just tell the students that based on the slant of the truncated conical cup, the complete cone would be 14 in tall and the part that was sliced off was 10 inches tall. (See solution for an explanation.) There is a worthwhile discussion to be had about parts (c) and (e). The percentage increase is smaller for the snow cones than it was for the juice treats. The snow cones have volume which is equal to those of the juice treats plus the volume of the dome, which is the same in both cases. Adding the same number to two numbers in a ratio will always make their ratio closer to one, which in this case means that the ratio - and thus percentage increase - would be smaller. |
| Flower Vases: | The purpose of this task is to give students practice working the formulas for the volume of cylinders, cones and spheres, in an engaging context that provides and opportunity to attach meaning to the answers. |
| Shipping Rolled Oats: | Students should think of different ways the cylindrical containers can be set up in a rectangular box. Through the process, students should realize that although some setups may seem different, they result in a box with the same volume. In addition, students should come to the realization (through discussion and/or questioning) that the thickness of a cardboard box is very thin and will have a negligible effect on the calculations. |
| Name |
Description |
| How thick is a soda can? (Variation II): | This problem solving task asks students to explain which measurements are needed to estimate the thickness of a soda can. Multiple solution processes are presented. |
| Archimedes and the King's Crown: | This problem solving task uses the tale of Archimedes and the King of Syracuse's crown to determine the volume and mass of gold and silver. |
| Doctor's Appointment: | The purpose of the task is to analyze a plausible real-life scenario using a geometric model. The task requires knowledge of volume formulas for cylinders and cones, some geometric reasoning involving similar triangles, and pays attention to reasonable approximations and maintaining reasonable levels of accuracy throughout. |
| Centerpiece: | The purpose of this task is to use geometric and algebraic reasoning to model a real-life scenario. In particular, students are in several places (implicitly or explicitly) to reason as to when making approximations is reasonable and when to round, when to use equalities vs. inequalities, and the choice of units to work with (e.g., mm vs. cm). |
| Use Cavalieri’s Principle to Compare Aquarium Volumes: | This task presents a context that leads students toward discovery of the formula for calculating the volume of a sphere. |
| Tennis Balls in a Can: | This task is inspired by the derivation of the volume formula for the sphere. If a sphere of radius 1 is enclosed in a cylinder of radius 1 and height 2, then the volume not occupied by the sphere is equal to the volume of a "double-naped cone" with vertex at the center of the sphere and bases equal to the bases of the cylinder |
| Glasses: | In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem. |
| Comparing Snow Cones: | Students will just be learning about similarity in this grade, so they may not recognize that it is needed in this context. Teachers should be prepared to give support to students who are struggling with this part of the task. To simplify the task, the teacher can just tell the students that based on the slant of the truncated conical cup, the complete cone would be 14 in tall and the part that was sliced off was 10 inches tall. (See solution for an explanation.) There is a worthwhile discussion to be had about parts (c) and (e). The percentage increase is smaller for the snow cones than it was for the juice treats. The snow cones have volume which is equal to those of the juice treats plus the volume of the dome, which is the same in both cases. Adding the same number to two numbers in a ratio will always make their ratio closer to one, which in this case means that the ratio - and thus percentage increase - would be smaller. |
| Flower Vases: | The purpose of this task is to give students practice working the formulas for the volume of cylinders, cones and spheres, in an engaging context that provides and opportunity to attach meaning to the answers. |
| Shipping Rolled Oats: | Students should think of different ways the cylindrical containers can be set up in a rectangular box. Through the process, students should realize that although some setups may seem different, they result in a box with the same volume. In addition, students should come to the realization (through discussion and/or questioning) that the thickness of a cardboard box is very thin and will have a negligible effect on the calculations. |