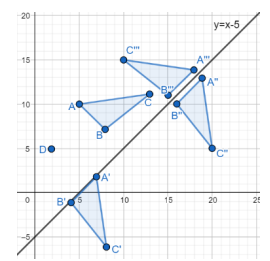
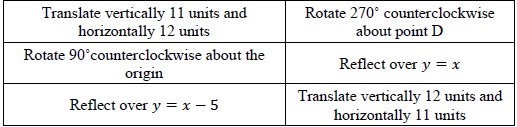
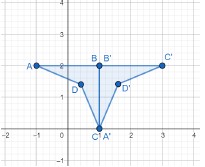
Identify a sequence of transformations that will map a given figure onto itself or onto another congruent or similar figure.
: Transformations include translations, dilations, rotations and reflections described using words or using coordinates.
| Name |
Description |
| "Triangle Congruence Show" Starring Rigid Transformations | Students will be introduced to the definition of congruence in terms of rigid motion and use it to determine if two triangles are congruent. |
| Sequence of Transformations | This lesson will assist students in performing multi-step transformations. Students will follow a sequence of transformations on geometric figures using translations, reflections, and rotations. |
| Regular Polygon Transformation Investigation | This is an introductory lesson on regular polygon transformation for congruency using a hands-on approach. |
| Match That! | Students will prove that two figures are congruent based on a rigid motion(s) and then identify the corresponding parts using paragraph proof and vice versa, prove that two figures are congruent based on corresponding parts and then identify which rigid motion(s) map the images. |
| Isometries with GeoGebra | In this lesson, students explore transformations with GeoGebra and then apply concepts using a straightedge on paper. Students apply rules for each isometry. There is a teacher-driven opening followed by individual student activity. |
| How Did It Get There? A Series of Transformation Events | Students will perform a series of transformations in order to determine how the pre-image will map onto the final image of a given figure. Students will use patty paper to manipulate their pre-image onto the image. Students will also work in collaborative groups to discuss their findings and will have the opportunity to share their series of transformations with the class. The class discussion will be used to demonstrate that there are several ways for the students to map their pre-image onto the final image. |
| Rotations of Regular Polygons | This lesson guides students through the development of a formula to find the first angle of rotation of any regular polygon to map onto itself. Free rotation simulation tools such as GeoGebra, are used. |
| Dancing For Joy | We have danced our way through reflections, rotations, and translations; now we are ready to take it up a notch by performing a sequence of transformations. Students will also discover the results when reflecting over parallel lines versus intersecting lines. |
| Turning to Congruence | This lesson uses rigid motions to prove the ASA and HL triangle congruence theorems. |
| Product of Two Transformations | Students will identify a sequence of steps that will translate a pre-image to its image. Students will also demonstrate that the sequence of two transformations is not always commutative. |
| Slip, Slide, Tip, and Turn: Corresponding Angles and Corresponding Sides | Using the definition of congruence in terms of rigid motion, students will show that two triangles are congruent. |
| How to Land Your Spaceship | Teach your students to maneuver a "spaceship" through a sequence of transformations that will successfully carry it onto its landing pad. GeoGebra directons are provided. |
| Exploring Congruence Using Transformations | This is an exploratory lesson that elicits the relationship between the corresponding sides and corresponding angles of two congruent triangles. |
| How do your Air Jordans move? | In this inquiry lesson, students are moving their individually designed Air Jordans around the room to explore rigid transformations on their shoes. They will Predict-Observe-Explain the transformations and then have to explain their successes/failures to other students. |
| I Am Still Me Transformed. | Students explore ways of applying, identifying, and describing reflection and rotation symmetry for both geometric and real-world objects, for them to develop a better understanding of symmetries in transformational geometry. |
| Triangles on a Lattice | In this activity, students will use a 3x3 square lattice to study transformations of triangles whose vertices are part of the lattice. The tasks include determining whether two triangles are congruent, which transformations connect two congruent triangles, and the number of non-congruent triangles (with vertices on the lattice) that are possible. |
| Rotations and Reflections of an Equilateral Triangle | Students will apply simple transformations (rotation and reflection) to an equilateral triangle, then determine the result of the action of two successive transformations, eventually determining whether the action satisfies the commutative and associate properties. |
| Reflections Hands On | Students will use a protractor/ruler to construct reflections and a composite of reflections. They will create transformations using paper cut-outs and a coordinate plane. For independent practice, students will predict and verify sequences of transformations. The teacher will need an LCD Projector and document camera. |
| Circle to Circle | Students use coordinate-based translations and dilations to prove circles are similar. |
| A Transformation's Adventure with Patty Paper: Exploring Translations, Reflections and Rotations. | Students are introduced to isometric transformations using patty paper. Translations, reflections, and rotations will be explained and practiced, emphasizing the properties preserved during those transformations and, without sacrificing precision, allowing students to differentiate between these isometries. The lesson can also be taught using GeoGebra free software. |
| Let's Reflect On This... | Students will use parallel and intersecting lines on the coordinate plane to transform reflections into translations and rotations. |
| Dilation Transformation | Students identify dilations, verify that polygons are similar, and use the dilation rule to map dilations. Task cards are provided for independent practice. The PowerPoint also includes detailed illustrations for constructing a dilation using a compass and a straight edge. |
| Transformers 3 | Students will learn the vocabulary of three rigid transformations, reflection, translation, and rotation, and how they relate to congruence. Students will practice transforming figures by applying each isometry and identifying which transformation was used on a figure. The teacher will assign students to take pictures of the three transformations found in the real world. |
| Transform through the Maze | In this fun activity, students will use rigid transformations to move a triangle through a maze. The activity provides applications for both honors and standard levels. It requires students to perform rotations, translations, and reflections. |
| Polygon Transformers | This guided discovery lesson introduces students to the concept that congruent polygons can be formed using a series of transformations (translations, rotations, reflections). As a culminating activity, students will create a robot out of transformed figures. |
| Rotations and Reflections of an Equilateral Triangle | Students will apply simple transformations (rotation and reflection) to an equilateral triangle, then determine the result of the action of two successive transformations, eventually determining whether the action satisfies the commutative and associate properties. |
| Name |
Description |
| Partitioning a Hexagon | The purpose of this task is for students to find a way to decompose a regular hexagon into congruent figures. This is meant as an instructional task that gives students some practice working with transformations. |
| Seven Circles II | This task provides a concrete geometric setting in which to study rigid transformations of the plane. |
| Congruent Segments | Students' first experience with transformations is likely to be with specific shapes like triangles, quadrilaterals, circles, and figures with symmetry. Exhibiting a sequence of transformations that shows that two generic line segments of the same length are congruent is a good way for students to begin thinking about transformations in greater generality. |
| Congruent Triangles | This task has two goals: first to develop student understanding of rigid motions in the context of demonstrating congruence. Secondly, student knowledge of reflections is refined by considering the notion of orientation in part (b). Each time the plane is reflected about a line, this reverses the notions of ''clockwise'' and ''counterclockwise.'' |
| Is This a Rectangle? | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Triangle congruence with coordinates | In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking. |
| Name |
Description |
| Partitioning a Hexagon: | The purpose of this task is for students to find a way to decompose a regular hexagon into congruent figures. This is meant as an instructional task that gives students some practice working with transformations. |
| Seven Circles II: | This task provides a concrete geometric setting in which to study rigid transformations of the plane. |
| Congruent Segments: | Students' first experience with transformations is likely to be with specific shapes like triangles, quadrilaterals, circles, and figures with symmetry. Exhibiting a sequence of transformations that shows that two generic line segments of the same length are congruent is a good way for students to begin thinking about transformations in greater generality. |
| Congruent Triangles: | This task has two goals: first to develop student understanding of rigid motions in the context of demonstrating congruence. Secondly, student knowledge of reflections is refined by considering the notion of orientation in part (b). Each time the plane is reflected about a line, this reverses the notions of ''clockwise'' and ''counterclockwise.'' |
| Is This a Rectangle?: | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Triangle congruence with coordinates: | In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking. |
| Name |
Description |
| Partitioning a Hexagon: | The purpose of this task is for students to find a way to decompose a regular hexagon into congruent figures. This is meant as an instructional task that gives students some practice working with transformations. |
| Seven Circles II: | This task provides a concrete geometric setting in which to study rigid transformations of the plane. |
| Congruent Segments: | Students' first experience with transformations is likely to be with specific shapes like triangles, quadrilaterals, circles, and figures with symmetry. Exhibiting a sequence of transformations that shows that two generic line segments of the same length are congruent is a good way for students to begin thinking about transformations in greater generality. |
| Congruent Triangles: | This task has two goals: first to develop student understanding of rigid motions in the context of demonstrating congruence. Secondly, student knowledge of reflections is refined by considering the notion of orientation in part (b). Each time the plane is reflected about a line, this reverses the notions of ''clockwise'' and ''counterclockwise.'' |
| Is This a Rectangle?: | The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem. |
| Triangle congruence with coordinates: | In this resource, students will decide how to use transformations in the coordinate plane to translate a triangle onto a congruent triangle. Exploratory examples are included to prompt analytical thinking. |