Standard #: MA.912.GR.1.4


This document was generated on CPALMS - www.cpalms.org



Prove relationships and theorems about parallelograms. Solve mathematical and real-world problems involving postulates, relationships and theorems of parallelograms.


Clarifications


Clarification 1: Postulates, relationships and theorems include opposite sides are congruent, consecutive angles are supplementary, opposite angles are congruent, the diagonals of a parallelogram bisect each other, and rectangles are parallelograms with congruent diagonals.

Clarification 2: Instruction includes constructing two-column proofs, pictorial proofs, paragraph and narrative proofs, flow chart proofs or informal proofs.

Clarification 3: Instruction focuses on helping a student choose a method they can use reliably.



General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 912
Strand: Geometric Reasoning
Standard: Prove and apply geometric theorems to solve problems.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Angle 
  • Parallelogram 
  • Quadrilateral 
  • Rectangle 
  • Rhombus 
  • Square 
  • Supplementary Angles

 

Vertical Alignment

Previous Benchmarks

Next Benchmarks

 

Purpose and Instructional Strategies

In elementary grades, students identified and classified quadrilaterals, including parallelograms. In grade 7, students solved problems involving the area of parallelograms. In Geometry, students establish relationships between sides, angles and diagonals of parallelograms (including the special cases of parallelograms: rectangles, rhombi and squares), prove the theorems related to these relationships and use them to solve mathematical and real-world problems. In later courses, parallelograms play an important role in work with vectors. 
  • Relationships, postulates and theorems in this benchmark should focus on, but are not limited to, the ones stated in Clarification 1. Additionally, some postulates and theorems have a converse (i.e., if conclusion, then hypothesis) that can be included. 
  • Instruction includes the connection to the Logic and Discrete Theory benchmarks when developing proofs. Additionally, with the construction of proofs, instruction reinforces the Properties of Operations, Equality and Inequality. (MTR.5.1) 
  • Instruction utilizes different ways students can organize their reasoning by constructing various proofs when proving geometric statements. It is important to explain the terms statements and reasons, their roles in a geometric proof, and how they must correspond to each other. Regardless of the style, a geometric proof is a carefully written argument that begins with known facts, proceeds from there through a series of logical deductions, and ends with the statement you are trying to prove. (MTR.2.1) 
    • For examples of different types of proofs, please see MA.912.LT.4.8. 
  • Instruction includes the connection to compass and straight edge constructions and how the validity of the construction is justified by a proof. (MTR.5.1) 
  • Students should develop an understanding for the difference between a postulate, which is assumed true without a proof, and a theorem, which is a true statement that can be proven. Additionally, students should understand why relationships and theorems can be proven and postulates cannot. 
  • Instruction includes the use of hatch marks, hash marks, arc marks or tick marks, a form of mathematical notation, to represent segments of equal length or angles of equal measure in diagrams and images. 
  • Students should understand the difference between congruent and equal. If two segments are congruent (i.e., PQ ≅ MN), then they have equivalent lengths (i.e., PQ = MN) and the converse is true. If two angles are congruent (i.e., ∠ABC ≅ ∠PQR), then they have equivalent angle measure (i.e., m∠ABC = m∠PQR) and the converse is true. 
  • Instruction includes the use of hands-on manipulatives and geometric software for students to explore relationships, postulates and theorems. 
  • Instruction includes discussing that the definition of a parallelogram only states that the opposite sides are parallel; anything else (e.g., opposite sides are congruent or opposite angles are congruent) is a property and needs to be proven. Students should understand that all parallelograms are trapezoids based on the definition within the K-12 Glossary. 
  • Instruction includes the connection to triangle congruence and the relationship between angles formed by a transversal through parallel lines when completing proofs about parallelograms. 
  • When the properties of parallelograms are introduced and proven, it is important to discuss the definitions of rectangles, rhombi and squares. Precision and accuracy are important when discussing the definitions of the special parallelograms. (MTR.3.1, MTR.4.1) 
    • For example, some possible discussion questions include: 
      • What makes a parallelogram a rectangle? 
      • What is the unique feature of a rhombus? 
      • Is a square always a rectangle? 
      • Is a square sometimes a rhombus? 
      • Is a rectangle always a square? Is a rhombus always a square? 
      • What are the properties of a parallelogram observed in a rhombus? 
  • Instruction includes proving that the diagonals of a parallelogram bisect each other and that the diagonals of a parallelogram are congruent if and only if the parallelogram is a rectangle. Clarify that just having congruent diagonals will not be enough to identify a quadrilateral as a rectangle as this is also a property of isosceles trapezoids. The quadrilateral has to be proven a parallelogram to use this property to classify it as a rectangle. 
  • Instruction includes the understanding that properties of parallelograms apply to all parallelograms, including squares, rhombi and rectangles.

 

Common Misconceptions or Errors

  • Students may think of squares, parallelograms, rectangles and rhombi as being exclusive to each other. A square is a rectangle and a rhombus. 
  • Students may think that parallelograms are not trapezoids. The K-12 Mathematics Glossary defines trapezoids as quadrilaterals with at least one pair of parallel sides. Therefore, all parallelograms are trapezoids.

 

Instructional Tasks

Instructional Task 1 (MTR.3.1) 
  • Given parallelogram ABCD, prove that angle A and angle B are supplementary. 
    parallelogram
Instructional Task 2 (MTR.4.1) 
  • Given quadrilateral JKLM with JK ≅ LM ≅ MJ.
 
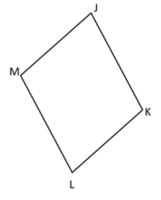
  • Part A. Draw the diagonal connecting points M and K. Determine and prove that two triangles are congruent. 
  • Part B. Using the congruent triangles from Part A, what is true about segments MJ and LK? 
  • Part C. Prove that quadrilateral JKLM is a parallelogram.

 

Instructional Items

Instructional Item 1 
  • Given parallelogram WXYZ, where WX = 2x + 15, XY = x + 27 and YZ = 4x − 21, determine the length of ZW, in inches.

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.


Related Courses

Course Number1111 Course Title222
1200400: Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206310: Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206320: Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206315: Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7912065: Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.912.GR.1.AP.4 Use the relationships and theorems about parallelograms. Solve mathematical and/or real-world problems involving postulates, relationships and theorems of parallelograms.


Related Resources

Formative Assessments

Name Description
Comparing Lengths in a Parallelogram

Students are given parallelogram ABCD along with midpoint E of diagonal AC and are asked to determine the relationship between the lengths AE + ED and BE + EC.

Finding Angle C

Students are given expressions that represent the measures of two angles of a parallelogram and are asked to find the measure of an angle opposite one of the given angles.

Frame It Up

Students are asked to explain how to determine whether a four-sided frame is a rectangle using only a tape measure.

Two Congruent Triangles

Students are asked to explain why a pair of triangles formed by the sides and diagonals of a parallelogram are congruent.

Angles of a Parallelogram

Students are given expressions that represent the measures of two angles of a parallelogram and are asked to find the measures of all four angles describing any theorems used.

Proving Congruent Diagonals

Students are asked to prove that the diagonals of a rectangle are congruent.

Proving a Rectangle Is a Parallelogram

Students are asked to prove that a rectangle is a parallelogram.

Proving Parallelogram Angle Congruence

Students are asked to prove that opposite angles of a parallelogram are congruent.

Proving Parallelogram Diagonals Bisect

Students are asked to prove that the diagonals of a parallelogram bisect each other.

Proving Parallelogram Side Congruence

Students are asked to prove that opposite sides of a parallelogram are congruent.

Prove Rhombus Diagonals Bisect Angles

Students are asked to prove a specific diagonal of a rhombus bisects a pair of angles.

Lesson Plans

Name Description
Proof of Quadrilaterals in Coordinate Plane

This lesson is designed to instruct students on how to identify special quadrilaterals in the coordinate plane using their knowledge of distance formula and the definitions and properties of parallelograms, rectangles, rhombuses, and squares. Task cards, with and without solution-encoded QR codes, are provided for cooperative group practice. The students will need to download a free "QR Code Reader" app onto their SmartPhones if you choose to use the cards with QR codes.

To Be or Not to Be a Parallelogram

Students apply parallelogram properties and theorems to solve real world problems. The acronym, P.I.E.S. is introduced to support a problem solving strategy, which involves drawing a Picture, highlighting important Information, Estimating and/or writing equation, and Solving problem.

Diagonally Half of Me!

This lesson is an exploration activity assisting students prove that diagonals of parallelograms bisect each other. It allows them to compare other quadrilaterals with parallelograms in order to make conjectures about the diagonals of parallelograms.

Who Am I?: Quadrilaterals

Students will use formulas they know (distance, midpoint, and slope) to classify quadrilaterals.

Proving Parallelograms Algebraically

This lesson reviews the definition of a parallelogram and related theorems. Students use these conditions to algebraically prove or disprove a given quadrilateral is a parallelogram.

Proving quadrilaterals algebrically using slope and distance formula

Working in groups, students will prove the shape of various quadrilaterals using slope, distance formula, and polygon properties. They will then justify their proofs to their classmates.

Quadrilaterals and Coordinates

In this lesson, students will use coordinates to algebraically prove that quadrilaterals are rectangles, parallelograms, and trapezoids. A through introduction to writing coordinate proofs is provided as well as plenty of practice.

Proving Quadrilaterals

This lesson provides a series of assignments for students at the Getting Started, Moving Forward, and Almost There levels of understanding for the Mathematics Formative Assessment System (MFAS) Task Describe the Quadrilateral (CPALMS Resource ID#59180). The assignments are designed to "move" students from a lower level of understanding toward a complete understanding of writing a coordinate proof involving quadrilaterals.

What's the Point?

Students will algebraically find the missing coordinates to create a specified quadrilateral using theorems that represent them, and then algebraically prove their coordinates are correct.

Note: This is not an introductory lesson for this standard.

Polygon...Prove it

While this is an introductory lesson on the standard, students will enjoy it, as they play "Speed Geo-Dating" during the Independent practice portion. Students will use algebra and coordinates to prove rectangles, rhombus, and squares. Properties of diagonals are not used in this lesson.

Perspectives Video: Teaching Idea

Name Description
Perpendicular Bisectors & Constructions

Unlock an effective teaching strategy for teaching geometric constructions, specifically perpendicular bisectors, in this Teacher Perspectives video for educators.

Problem-Solving Tasks

Name Description
Midpoints of the Side of a Parallelogram

This is a reasonably direct task aimed at having students use previously-derived results to learn new facts about parallelograms, as opposed to deriving them from first principles.

Inscribing a square in a circle

This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context.

Is This a Rectangle?

The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem.

Student Resources

Problem-Solving Tasks

Name Description
Midpoints of the Side of a Parallelogram:

This is a reasonably direct task aimed at having students use previously-derived results to learn new facts about parallelograms, as opposed to deriving them from first principles.

Inscribing a square in a circle:

This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context.

Is This a Rectangle?:

The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem.



Parent Resources

Problem-Solving Tasks

Name Description
Midpoints of the Side of a Parallelogram:

This is a reasonably direct task aimed at having students use previously-derived results to learn new facts about parallelograms, as opposed to deriving them from first principles.

Inscribing a square in a circle:

This task provides an opportunity for students to apply triangle congruence theorems in an explicit, interesting context.

Is This a Rectangle?:

The goal of this task is to provide an opportunity for students to apply a wide range of ideas from geometry and algebra in order to show that a given quadrilateral is a rectangle. Creativity will be essential here as the only given information is the Cartesian coordinates of the quadrilateral's vertices. Using this information to show that the four angles are right angles will require some auxiliary constructions. Students will need ample time and, for some of the methods provided below, guidance. The reward of going through this task thoroughly should justify the effort because it provides students an opportunity to see multiple geometric and algebraic constructions unified to achieve a common purpose. The teacher may wish to have students first brainstorm for methods of showing that a quadrilateral is rectangle (before presenting them with the explicit coordinates of the rectangle for this problem): ideally, they can then divide into groups and get to work straightaway once presented with the coordinates of the quadrilateral for this problem.



Printed On:4/20/2024 10:33:59 AM
Print Page | Close this window