General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Event
- Experimental Probability
- Simulation
- Theoretical Probability
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
In grade 7, students use a simulation of a simple experiment to find experimental probabilities and compare them to theoretical probabilities. In grade 8, students will solve real-world problems involving probabilities related to single or repeated experiments, including making predictions based on theoretical probability.- Instruction includes opportunities for students to run various numbers of trials to discover that the increased repetition of the experiment will bring the experimental probability closer to the theoretical. Use virtual simulations to quickly show higher and higher volumes of repetition that would be difficult to create with physical manipulatives (MTR.5.1).
- Remind students that chance has no memory and each repetition in the simulation has the same probability distribution for the possible events.
- For example, if you flip a coin and it lands on heads, the next flip does not rely on the first outcome and still can be either heads or tails.
- Instruction focuses on the simple experiments listed in Clarification 3.
- For example, students can roll a 6-sided die 30 times to determine the experimental probability of “not rolling a 2.” Students can then compare their experimental probability to the theoretical probability of “not rolling a 2,” which is .
Common Misconceptions or Errors
- Students may incorrectly assume the theoretical and experimental probabilities of the same experiment will always be the same. To address this misconception, provide multiple opportunities for students to experience simulations of different situations, with physical or virtual manipulatives, in order to find and compare the experimental and theoretical probabilities.
- Students may incorrectly expect to see every possible outcome occur during a simulation. While all may occur in a simulation, it is not certain to happen. Students may inadvertently let their own experience with an experiment affect their response.
- For example, during an experiment if a student never draws an ace from a standard deck of cards, this does not indicate it could never happen.
Strategies to Support Tiered Instruction
- Teacher reviews the root words theoretical (theory) and experimental (experiment) and discusses the difference between a theoretical probability and experimental probability. Teacher provides graphic organizer to keep as reference for root words.
- For example, experimental probabilities are from simulations whereas theoretical probabilities are from calculations.
- Teacher provides opportunities to see a variety of outcomes.
- For example, open a deck of cards and draw 5 random cards. After looking at the 5 cards, discuss all the possible cards that could have been drawn but were not. This will help students see that not all possible outcomes will occur when an experiment is done.
- Teacher provides multiple examples for students to discuss if a probability in the example is theoretical or experimental. After each answer, students discuss how they know it is theoretical or experimental.
- For example, if one tosses a fair coin, the theoretical probability of landing on heads is 0.5. If one tosses a fair coin 14 times and it lands on hands 9 times, the experimental probability of landing on heads is based on the simulation.
- Teacher provides multiple opportunities for students to experience simulations of different situations, with physical or virtual manipulatives, in order to find and compare the experimental and theoretical probabilities.
Instructional Tasks
Instructional Task 1 (MTR.4.1)Each set of partners has been given a bag containing 5 red, 5 green, 5 yellow and 10 brown candies.
- Part A. Determine the theoretical probability for selecting one red candy at random from the bag. Do the same for blue, yellow and brown.
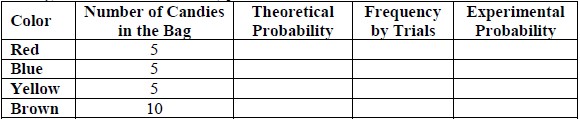
- Part B. Experimental Trials: Select one candy from the bag, record its color in the table below and return it to the bag. Repeat this process for a total of 20 trials.
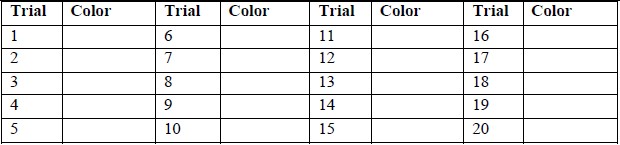
- Part C. In the original table, record the total frequency of each color based on your 20 trials. Then calculate the experimental probability for each. How do the theoretical and experimental probabilities compare?
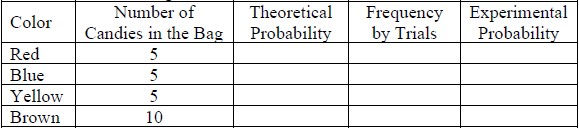
- Part D. Collect the data from 2 other sets of partners and combine your total frequencies. Complete the table below based on those 60 trials. How do the theoretical and experimental probabilities compare? How does that compare to your original calculations using 20 trials?
- Part E. Collect all of the class data to calculate new total frequencies and complete the table below.
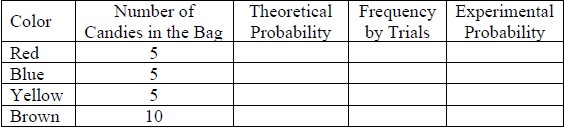
- Part F.
- How do the theoretical and experimental probabilities compare?
- How does that compare to the calculations using 20 trials and 60 trials?
- What conclusions can you make about theoretical and experimental probabilities based on this information?
Instructional Items
Instructional Item 1A bag contains green marbles and purple marbles. If a marble is randomly selected from the bag, the probability that it is green is 0.6 and the probability that it is purple is 0.4. Dylan draws a marble from the bag, notes its color, and returns it to the bag. He does this 50 times. Approximately, how many times would you expect Dylan to draw a green marble?
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
