Standard #: MA.7.GR.2.3


This document was generated on CPALMS - www.cpalms.org



Solve mathematical and real-world problems involving volume of right circular cylinders.


Clarifications


Clarification 1: Within this benchmark, the expectation is not to memorize the volume formula for a right circular cylinder or to find radius as a missing dimension.

Clarification 2: Solutions may be represented in terms of pi (π) or approximately.



General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 7
Strand: Geometric Reasoning
Standard: Solve problems involving three-dimensional figures, including right circular cylinders.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Cylinder (Circular)
  • Pi (π)
  • Volume

 

Vertical Alignment

Previous Benchmarks

Next Benchmarks

 

Purpose and Instructional Strategies

Students progress through solving problems involving volumes with a focus of right rectangular prisms in grade 6, right circular cylinders in grade 7 and cylinders, pyramids, prisms, cones and spheres in high school. 
  • Instruction builds on students’ knowledge of finding the volume of a rectangular prism, which also includes the area of the base multiplied by the height. Ask students to make conjectures about how to calculate the volume of a right circular cylinder. Provide the radius and height of several cylinders for students to verify or revise their conjecture (MTR.6.1).
  • Instruction includes physical or virtual representations for the volume of a right circular cylinder (MTR.2.1).
    • For example, stack quarters one at a time to show repeated addition (the height) on the area of the base (the first quarter used).
  • Instruction focuses on real-world situations to reinforce conceptual understanding of volume versus surface area (MTR.7.1).

 

Common Misconceptions or Errors

  • Students often confuse the vocabulary base, length, height and “B” (base area), when moving between two-and three-dimensional figures. To address this misconception, continue to use the parts of the net to calculate the surface area, rather than focusing on the formula.
  • Students may incorrectly believe that whatever is lying flat is the base of the figure. To address this misconception, remind students that while a cylinder may lay on its side, the bases are the circles with the height being the perpendicular distance between them. Provide multiple orientations of objects and continue to break them down to their nets.
  • Students may incorrectly apply the formulas for area, surface area and volume.

 

Strategies to Support Tiered Instruction

  • Instruction includes the use of geometric software to allow students to explore the difference between base, length, height, and “B” (base area).
  • Teacher creates and posts an anchor chart with visual representations of a right circular cylinder to assist in correct academic vocabulary when solving real-world problems.
  • Teacher provides students with an example of a three-dimensional figure in its original position then provides multiple orientations to discuss how the location of the figure’s base changes, but the dimensions of the figure do not change.
    • For example, two right circular cylinders are shown below with the same dimensions but in different orientations. The base is highlighted in each.
      Cylinders
  • Teacher instructs students to draw a visual of a three-dimensional figure and its dimensions in the context of a real-world problem.
  • Instruction includes opportunities for students to solve for the volume of a given right circular cylinder in terms of pi before replacing the value of pi with an approximation to determine the estimated volume.
  • Instruction includes co-constructing a graphic organizer of a right circular cylinder and color-coding and labeling the dimensions.
  • Teacher provides instruction focused on manipulatives or geometric software for students to develop understanding of the difference between the formulas for area, surface area and volume.
  • Teacher provides opportunities for students to comprehend the context or situation by engaging in questions (laminating these questions on a printed card for students to utilize as a resource in and out of the classroom would be helpful).
    • What do you know from the problem?
    • What is the problem asking you to find?
    • Can you create a visual model to help you understand or see patterns in your problem?
  • Teacher encourages students to continue to use the parts of the net to calculate the surface area, rather than focusing on the formula.
  • Teacher reminds students that while a cylinder may lay on its side, the bases are the circles with the height being the perpendicular distance between them. Provide multiple orientations of objects and continue to break them down to their nets.

 

Instructional Tasks

Instructional Task 1 (MTR.1.1)
Coffee2Go wants to build a record breaking giant coffee cup for a promotional celebration at a convention for coffee drinkers. In 2020, the Guinness Book of World Records reported that the World’s Largest Cup of Coffee contained 2,010 gallons of fresh-brewed coffee brewed.
  • Part A. What questions would need to be answered to approach this problem? Do you have all the information you need to solve the problem? Why or why not?
  • Part B. The Guinness Book of World Records, in 2020, documented the Largest Coffee Cup with a height of 8 feet and a diameter of 8 feet. How many cubic feet of coffee can be held in the World’s Largest Coffee Cup?
  • Part C. There are approximately 1.25 gallons of coffee in a cubic foot. If Coffee2Go has a goal of creating a coffee cup that holds 2,410 gallons of coffee, what could be the height and diameter of the coffee cup if they are the same size?

Instructional Task 2 (MTR.7.1)
Karim is setting up an inflatable pool in the yard for the little kids to play. The pool measures 312 feet across and 16 inches deep. What is the volume of water needed to fill the pool all the way to the top?

 

Instructional Items

Instructional Item 1
What is the height of a cylinder, with a radius of 3.4 meters (m), whose volume is 198 m³? Round to the nearest hundredth.

Instructional Item 2
Determine the exact volume of each of the following cylinders.
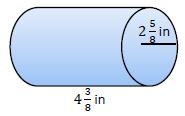
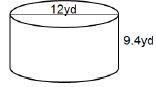
Cylinder

Cylinder


Instructional Item 3
A candle mold has 24π in³ of space in which wax can be poured to make a candle. If the radius of the mold is 2 inches (in), what is its height?

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.



Related Courses

Course Number1111 Course Title222
1205040: M/J Grade 7 Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1205050: M/J Accelerated Mathematics Grade 7 (Specifically in versions: 2014 - 2015, 2015 - 2020, 2020 - 2022, 2022 and beyond (current))
1204000: M/J Foundational Skills in Mathematics 6-8 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7812020: Access M/J Grade 7 Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2019, 2019 - 2022, 2022 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.7.GR.2.AP.3 Given a formula, use tools to calculate the volume of right circular cylinders.


Related Resources

Formative Assessment

Name Description
Platinum Cylinder

Students are asked to solve a problem that requires calculating the volume of a cylinder.

Lesson Plans

Name Description
How Many Cones Does It Take?

This lesson is a "hands-on" activity. Students will investigate and compare the volumes of cylinders and cones with matching radii and heights. Students will first discover the relationship between the volume of cones and cylinders and then transition into using a formula to determine the volume.

Find your Formula!

Students will investigate the formula for the volume of a pyramid and/or cone and use those formulas to calculate the volume of other solids. The students will have hands-on discovery working with hollow Geometric Solids that they fill with dry rice, popcorn, or another material.

Silly Cylinders

This is a short activity where students determine the density of the human body by considering each part of the body to be a cylinder. I use this activity during the second week of school, so students have already had some practice with measurement. In addition to providing students with practice in data collection and problem solving, it is a good activity that allows teachers to measure students' previous knowledge in these areas.

The Cost of Keeping Cool

Students will find the volumes of objects. After decomposing a model of a house into basic objects students will determine the cost of running the air conditioning.

Victorious with Volume

In this lesson, the students will explore and use the relationship of volume for cylinders and cones that have equal heights and radii.

M&M Soup

This is the informative part of a two-lesson sequence. Students explore how to find the volume of a cylinder by making connections with circles and various real-world items.

A Pi-ece of Florida History

A Pi-ece of Florida History discovers significant dates in Florida History in the first 8 digits after the decimal of the number Pi. Historical people associated with those dates are identified and described. Students then use body measurements to approximate volume.

Relating Surface Area and Volume

Students will recognize that while the surface area may change, the volume can remain the same. This lesson is enhanced through the multimedia CPALMS Perspectives Video, which introduces students to the relationship between surface area and volume.

Perspectives Video: Professional/Enthusiasts

Name Description
Volume and Surface Area of Pizza Dough

Michael McKinnon of Gaines Street Pies explains how when making pizza the volume is conserved but the surface area changes.

KROS Pacific Ocean Kayak Journey: Food Storage Mass and Volume

What do you do if you don't have room for all your gear on a solo ocean trek? You're gonna need a bigger boat...or pack smarter with math.

Related Resources:
KROS Pacific Ocean Kayak Journey: GPS Data Set[.XLSX]
KROS Pacific Ocean Kayak Journey: Path Visualization for Google Earth[.KML]

Download the CPALMS Perspectives video student note taking guide.

Perspectives Video: Teaching Idea

Name Description
Surface Area Misconception

Unlock an effective teaching strategy for identifying the base and height of figures in this Teacher Perspectives video for educators.

Problem-Solving Tasks

Name Description
How thick is a soda can? (Variation II)

This problem solving task asks students to explain which measurements are needed to estimate the thickness of a soda can. Multiple solution processes are presented.

Glasses

In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem.

Comparing Snow Cones

Students will just be learning about similarity in this grade, so they may not recognize that it is needed in this context. Teachers should be prepared to give support to students who are struggling with this part of the task. To simplify the task, the teacher can just tell the students that based on the slant of the truncated conical cup, the complete cone would be 14 in tall and the part that was sliced off was 10 inches tall. (See solution for an explanation.) There is a worthwhile discussion to be had about parts (c) and (e). The percentage increase is smaller for the snow cones than it was for the juice treats. The snow cones have volume which is equal to those of the juice treats plus the volume of the dome, which is the same in both cases. Adding the same number to two numbers in a ratio will always make their ratio closer to one, which in this case means that the ratio - and thus percentage increase - would be smaller.

Shipping Rolled Oats

Students should think of different ways the cylindrical containers can be set up in a rectangular box. Through the process, students should realize that although some setups may seem different, they result in a box with the same volume. In addition, students should come to the realization (through discussion and/or questioning) that the thickness of a cardboard box is very thin and will have a negligible effect on the calculations.

Unit/Lesson Sequence

Name Description
Three Dimensional Shapes

In this interactive, self-guided unit on 3-dimensional shape, students (and teachers) explore 3-dimensional shapes, determine surface area and volume, derive Euler's formula, and investigate Platonic solids. Interactive quizzes and animations are included throughout, including a 15 question quiz for student completion.

Student Resources

Problem-Solving Tasks

Name Description
How thick is a soda can? (Variation II):

This problem solving task asks students to explain which measurements are needed to estimate the thickness of a soda can. Multiple solution processes are presented.

Glasses:

In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem.

Comparing Snow Cones:

Students will just be learning about similarity in this grade, so they may not recognize that it is needed in this context. Teachers should be prepared to give support to students who are struggling with this part of the task. To simplify the task, the teacher can just tell the students that based on the slant of the truncated conical cup, the complete cone would be 14 in tall and the part that was sliced off was 10 inches tall. (See solution for an explanation.) There is a worthwhile discussion to be had about parts (c) and (e). The percentage increase is smaller for the snow cones than it was for the juice treats. The snow cones have volume which is equal to those of the juice treats plus the volume of the dome, which is the same in both cases. Adding the same number to two numbers in a ratio will always make their ratio closer to one, which in this case means that the ratio - and thus percentage increase - would be smaller.

Shipping Rolled Oats:

Students should think of different ways the cylindrical containers can be set up in a rectangular box. Through the process, students should realize that although some setups may seem different, they result in a box with the same volume. In addition, students should come to the realization (through discussion and/or questioning) that the thickness of a cardboard box is very thin and will have a negligible effect on the calculations.



Parent Resources

Problem-Solving Tasks

Name Description
How thick is a soda can? (Variation II):

This problem solving task asks students to explain which measurements are needed to estimate the thickness of a soda can. Multiple solution processes are presented.

Glasses:

In this resource, students will determine the volumes of three different shaped drinking glasses. They will need prior knowledge with volume formulas for cylinders, cones, and spheres, as well as experience with equation solving, simplifying square roots, and applying the Pythagorean theorem.

Comparing Snow Cones:

Students will just be learning about similarity in this grade, so they may not recognize that it is needed in this context. Teachers should be prepared to give support to students who are struggling with this part of the task. To simplify the task, the teacher can just tell the students that based on the slant of the truncated conical cup, the complete cone would be 14 in tall and the part that was sliced off was 10 inches tall. (See solution for an explanation.) There is a worthwhile discussion to be had about parts (c) and (e). The percentage increase is smaller for the snow cones than it was for the juice treats. The snow cones have volume which is equal to those of the juice treats plus the volume of the dome, which is the same in both cases. Adding the same number to two numbers in a ratio will always make their ratio closer to one, which in this case means that the ratio - and thus percentage increase - would be smaller.

Shipping Rolled Oats:

Students should think of different ways the cylindrical containers can be set up in a rectangular box. Through the process, students should realize that although some setups may seem different, they result in a box with the same volume. In addition, students should come to the realization (through discussion and/or questioning) that the thickness of a cardboard box is very thin and will have a negligible effect on the calculations.



Printed On:4/27/2024 3:51:50 AM
Print Page | Close this window