General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
- There are no direct connections outside of this standard; however, teachers are encouraged to find possible indirect connections.
Terms from the K-12 Glossary
- Acute Triangle
- Equilateral Triangle
- Isosceles Triangle
- Obtuse Triangle
- Parallelograms
- Quadrilateral
- Rectangle
- Rhombus
- Right Triangle
- Scalene Triangle
- Square
- Trapezoid
- Triangle
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to understand that shapes can be classified by their attributes and these attributes may place them in multiple categories. In grade 3, students identified and drew quadrilaterals based on their attributes (MA.3.GR.1.2). In grade 4, students explored angle classifications and measures in two-dimensional figures (MA.4.GR.1.1). This past work built the understanding required for students to classify triangles and quadrilaterals in grade 5. Classification of geometric figures will return in high school geometry (MA.912.GR.3.2) using another grade 5 concept, the coordinate plane.- The work in grade 5 will help students to understand that triangles can be defined by two different attributes that students can measure: the length of their sides (3 congruent sides, 2 congruent sides, or 0 congruent sides) and the size of their angle measures (3 acute angles, 2 acute angles and a right angle, or 2 acute angles and an obtuse angle).
- During instruction, it is important for students to have practice with classifying figures in multiple ways so they can better understand the relationship between attributes of the geometric figures. In addition, students should practice this concept by using graphic organizers such as, flow charts, T-charts and Venn diagrams (MTR.2.1).
- This benchmark requires a strong understanding and use of geometry vocabulary. Allow students to use math discourse throughout instruction to compare the attributes of geometric figures. o For example, pose questions such as, “Why is a square always a rhombus?” and “Why is a rhombus not always a square?” Lesson activities should require students to justify their thinking when making mathematical arguments about geometric figures (MTR.4.1).
Common Misconceptions or Errors
- Students may think that when describing and classifying geometric shapes and placing them in subcategories, the last subcategory is the only classification that can be used.
- Students may think that a geometric figure can only be classified in one way.
- For example, a square (a shape with 4 congruent sides and 4 congruent angles) can also be a parallelogram because it contains 2 pairs of sides that are congruent and parallel.
Strategies to Support Tiered Instruction
- Instruction includes providing a graphic organizer and having students place triangles and/or quadrilaterals into all the subcategories they belong to. Students then identify all the ways the figure could be classified.
- For example, students are provided with a graphic organizer like the one shown below to help them classify figures into subcategories. The name of the figure, an example, and the definition are provided. Students then identify which other categories the figure would also fit. For example, a parallelogram is a quadrilateral containing two pairs of parallel sides. A rectangle, rhombus, and square all also have two pairs of parallel sides so they would also fit in this subcategory. The teacher refers to the glossary, included with the standards, for several examples to provide students.
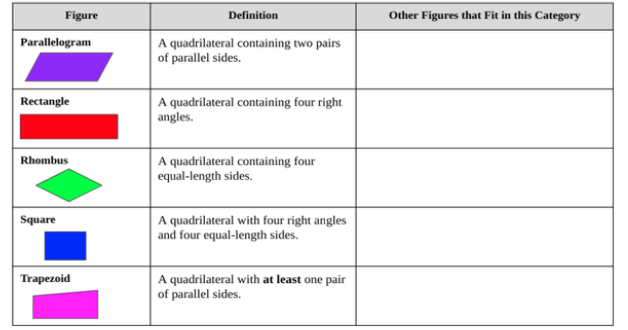
- Instruction includes providing a graphic organizer and having students use sticky notes with specific attributes on them to help them classify figures.
- For example, students are provided with a graphic organizer like the one shown below with an example of the figure filled in for them to refer to and yellow sticky notes that have “4 equal sides” written on them. Students determine which figures contain this attribute and place the sticky note under those figures (square and rhombus). The teacher then provides green sticky notes with “two pairs of parallel sides” written on them. Students place the sticky note under each figure that has that attribute (parallelogram, rhombus, rectangle, and square). Students would continue to add different color sticky notes with attributes that say, “One pair of parallel sides” and “four right angles”. Students are able to see that some figures have several sticky notes and which figures have the same sticky notes. Students will then name all the ways a figure can be classified based on the attributes they have.
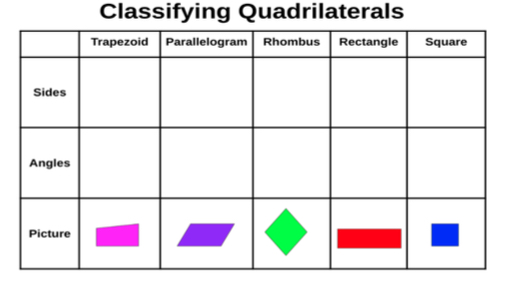
- Instruction may include providing a variety of graphic organizers that allow students to build physical and cognitive connections
- For example, have students create or provide them with a template to complete a double-bubble graphic organizer; then allow them to compare and contrast assorted examples.
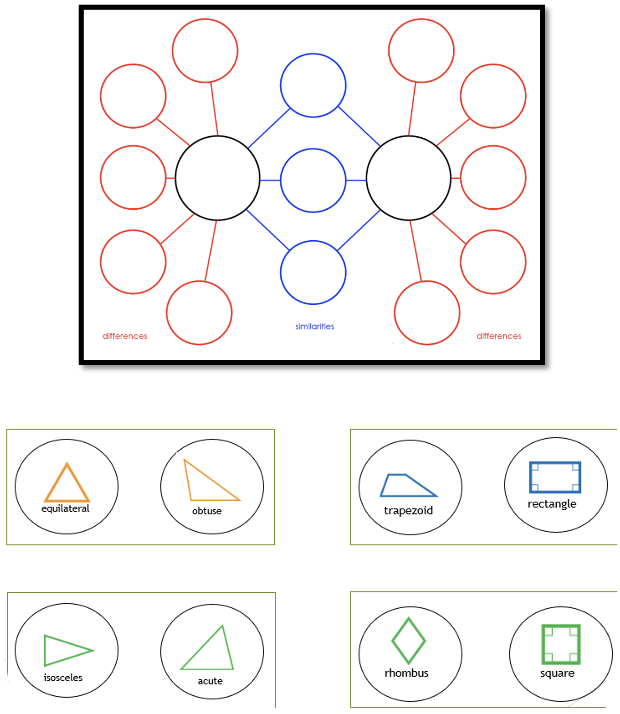
Instructional Tasks
Instructional Task 1 (MTR.3.1, MTR.4.1)
- Part A. Roll a number cube twice and write a statement based on the key below.
- Part B. Write a statement that reads, “A(n) ___________ (roll 1) triangle is ______________ (always, sometimes or never) a(n) ____________ triangle (roll 2).” Complete your statement by determining whether the category of triangle from roll 1 is always, sometimes, or never the category of triangle from roll 2. Complete this process three more times for a total of four statements.
- Part C. Choose one of the statements that you said is sometimes true. Give an example of when the statement is true and when the statement is not true using picture models or words. If none of your statements are sometimes true, then create one to give an example.
Instructional Items
Instructional Item 1
Choose all the shapes that can always be classified as parallelograms.- a. Trapezoid
- b. Rectangle
- c. Rhombus
- d. Square Equilateral Triangle
What type of triangle is shown?
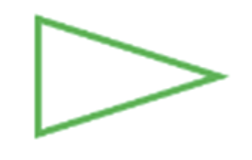
- a. Equilateral Triangle
- b. Isosceles Triangle
- c. Obtuse Triangle
- d. Scalene Triangle
Instructional Item 3
Which shape is an obtuse triangle?

Instructional Item 4
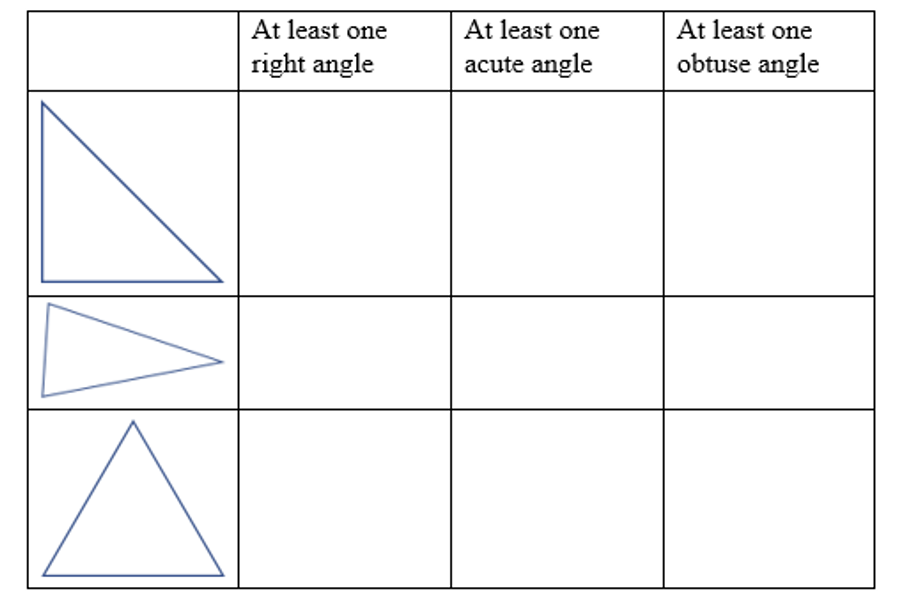
Using the table, identify the angles of the triangles by putting an X in the corresponding column.
Instructional Item 5
The figure below has equal side lengths. Classify the figure, selecting all that apply.

- a. Quadrilateral
- b. Rectangle
- c. Rhombus
- d. Square
- e. Trapezoid
Instructional Item 6
Which shape is a rhombus?

Instructional Item 7
Using the table, identify the angles of the triangles by putting an X in the corresponding column.
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.
