General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Equation
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is to continue the work from grade 4 where students began solving real-world with fractions, and prepares them for grade 6 (MA.6.NSO.2.3) where they will solve real-world fraction problems using all four operations with fractions (MTR.7.1).- Students need to develop an understanding that when adding or subtracting fractions, the fractions must refer to the same whole.
- During instruction, teachers can provide opportunities for students to practice solving problems using models or drawings to add, subtract or multiply with fractions. Begin with students modeling with whole numbers, have them explain how they used the model or drawing to arrive at the solution, then scaffold using the same methodology using fraction models. Instruction allows students to continue building an understanding of fraction operations through modeling and the use of manipulatives.
- Students are encouraged to express problem-solving solutions through various means, such as objects, illustrations, tables, graphs, and equations (MTR.2.1). When tackling fraction-related challenges, it is advisable to employ diverse models, including but not confined to area models (rectangles), linear models (fraction strips/bars and number lines), and set models (counters). There should be student progression from solving problems with physical manipulatives and illustrations to the utilization of algorithms and equations. Students should articulate the relationships between different concepts and representations, while also selecting the most suitable representation based on the specific context or purpose of the question.
- Please note that it is not expected for students to always find least common multiples or make fractions greater than 1 into mixed numbers, but it is expected that students know and understand equivalent fractions, including naming fractions greater than 1 as mixed numbers to add, subtract or multiply.
- It is important that teachers have students rename the fractions with a common denominator when solving addition and subtraction fraction problems, in lieu of using tricks, shortcuts, or mnemonics, to ensure students build a conceptual understanding.
Common Misconceptions or Errors
- When solving real-world problems, students can often confuse contexts that require subtraction and multiplication of fractions.
- For example, “Mark has yards of rope and he gives half of the rope to a friend. How much rope does Mark have left?” expects students to find of , or multiply × to find the product that represents how much is given to the friend. On the other hand, “Mark has yards of rope and gives yard of rope to a friend. How much rope does Mark have left?” expects students to take yard from yard, or subtract − to find the difference. Encourage students to look for the units in the problem (e.g., yard versus of the whole rope) to determine the appropriate operation.
- Students may believe that multiplication always results in a larger number. Using models when multiplying with fractions will enable students to generalize about multiplication algorithms that are based on conceptual understanding (MTR.5.1). Encourage students to use their number sense when determining the size of a product (connecting to MA.5.FR.2.3). The teacher can ask students what they know about multiplying fractions to determine how the numbers in the problem are related.
- Students can have difficulty with word problems when determining which operation to use, and the stress of working with fractions makes this happen more often. Students need to apply what they already know about operations with fractions to create action plans to solve multi-step real-world problems involving fractions.
- For example, “Mark has yards of rope and he gives a third of the rope to a friend. How much rope does Mark have left?” expects students to first find of , or multiply 1/3 × , and then to find the difference to find how much Mark has left. On the other hand, "Mark has yards of rope and gives yard of rope to a friend. How much rope does Mark have left?” only requires finding the difference − .
- With guiding questions, teachers can ask students what operation will be needed to solve the problem. Prompt students to indicate what the first action step will be before they solve. If students struggle to find the first step of the problem, encourage them to create a visual model while rereading.
Strategies to Support Tiered Instruction
- Instruction includes opportunities to identify the appropriate operation to use in a real- world problem that requires addition, subtraction, or multiplication of fractions. The teacher guides students to identify the units in the problem for clarification on which operation is appropriate.
- For example, the teacher displays and reads the following two problems:
- “Ganie has of a bar of chocolate left and gives half of what she has to her friend Sarah. How much of a whole chocolate bar does she have left?”
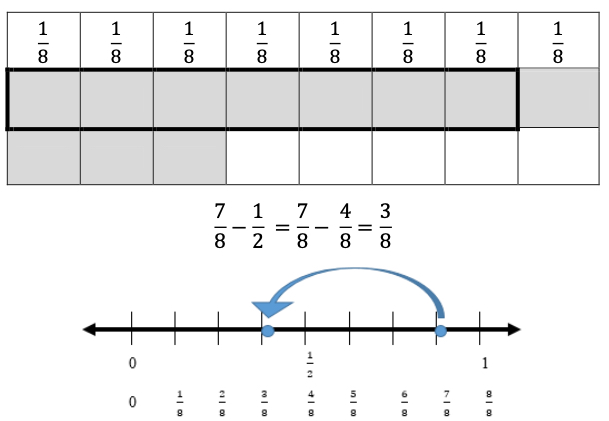
- “Ganie has of a bar of chocolate left and she gives of the original bar of chocolate to her friend Sarah. How much of her chocolate bar does she have left?” (See illustration below)
- The teacher uses questioning and prompting to have students identify what operations must be used to solve each problem. The teacher asks students to share what they notice about each problem (e.g., the similarities and the differences), placing emphasis on the units (e.g., “half of the amount of chocolate that Janie has in the first problem vs. of the whole chocolate bar” in the second problem). The teacher guides students to identify that in the first problem, they will need to multiply × and in the second problem, they will need to subtract − to solve. Students solve using models.
- For example, the teacher displays and reads the following two problems:
×=
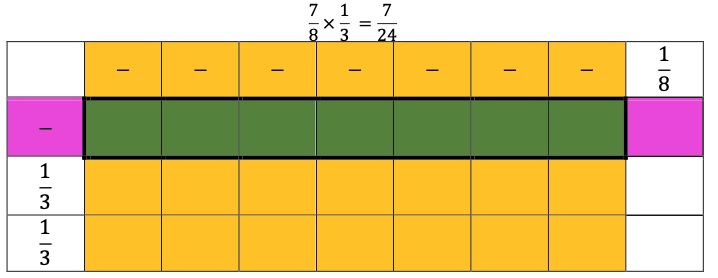
- For example, the teacher displays and reads the following problem: "Tia has yards of ribbon and she gives half of the ribbon to a friend. How much ribbon does Tia have left?” The teacher uses questioning and prompting to have students identify what operation must be used to solve the problem. The teacher asks students, “Did Tia give half of the ribbon or half a yard of ribbon to her friend?” Emphasis is placed on the units (e.g., half of the whole ribbon vs. yard of ribbon) while guiding students to identify that they will need to multiply × to solve. Students solve using the area model and counters. The cells with both color counters indicate the numerator in the solution. This is repeated with similar word problems, using frequent guiding questions to support student understanding.
-1.png)
- Instruction includes opportunities to use models when solving problems that involve multiplication of fractions to increase understanding that multiplication does not always result in a larger number. The use of models when multiplying with fractions will enable students to generalize about multiplication algorithms that are based on conceptual understanding.
- For example, the teacher displays and reads aloud the following problem: “Rosalind spent of an hour helping in the garden. Her sister spent the amount of time as Rosalind did helping in the garden. How much time did Rosalind’s sister spend helping in the garden?” Students solve the problem using an area model. The teacher uses questioning to help students draw a model to represent the problem. This is repeated with similar word problems involving multiplication of fractions.
- For example, the teacher displays and reads aloud the following problem: "Astrid spent of an hour reading her book. Elliot spent the amount of time as Astrid did reading. How much time did Elliot spend reading?” Students solve using the area model and counters. The cells with both color counters indicate the numerator in the solution. The teacher uses questioning to help students draw a model to represent the problem. This is repeated with similar word problems involving multiplication of fractions, using frequent guiding questions to support student understanding.
Instructional Tasks
Instructional Task 1 (MTR.7.1)
Rachel wants to bake her two favorite brownie recipes. One recipe needs 1 cups of flour and the other recipe needs cups of flour. How much flour does Rachel need to bake her two favorite brownie recipes?Instructional Task 2 (MTR.7.1)
Shawn finished a 100 meter race in of one minute. The winner of the race finished in of Shawn’s time. How long did it take for the winner of the race to finish?Instructional Task 3Megan has a collection of 80 stickers, and 1/5 of them feature cars, while 1/4 of the stickers have animals. The remaining stickers display various types of shapes. How many stickers in Megan’s collection feature shapes?
Instructional Task 4
Megan has a collection of 80 stickers, and 1/5 of them feature cars, while 1/4 of the stickers have animals. The remaining stickers display various types of shapes. How many stickers in Megan’s collection feature shapes?
Instructional Task 5 (MTR.7.1)
Some of the problems below can be solved by multiplying 1/4 ×3/5, while others require a different operation to solve. Select the situations that can be solved using the expression 1/4×3/5. For the other situations, indicate what operation is needed to solve, then solve.
a. One-fourth of the students in Gary’s fifth-grade class are boys. Three-fifths of the boys wear a blue shirt. What fraction of Gary’s class are boys wearing blue shirts?
b. A rectangular field is divided into two sections. One section is 1/4 of the total area, and the other section is 3/5 of the total area. What fraction of the field is left unoccupied?
c. There is 1/4 box of chocolates left over after a party. If George eats another 3/5 of the original box of chocolates, what fraction of the original box is left over?
d. A factory produces two types of products. One product is 1/4 of the factory's total production, and the other product is is 3/5 of the factory’s total production. What fraction of the total production is made up of these products combined?
e. A recipe calls for 1/4 cup of sugar. Mary wants to make 3/5 of the recipe. How much sugar, in cups, should Mary use in her scaled-down version of the recipe?
f. In a deck of cards, 1/4 of the cards are spades, and 3/5 of the spades are face cards (jack, queen, king). What fraction of the deck is a face card that is also a spade?
g. At the picnic, 1/4 of the attendees brought sandwiches, and 3/5 of those who brought sandwiches also brought drinks. What fraction of the attendees brought both sandwiches and drinks?
Instructional Items
Instructional Item 1
Monica has 2 cups of berries. She uses cups of berries to make a smoothie. She then uses cup for a fruit salad. After she makes her smoothie and fruit salad, how much of the berries will Monica have left?Instructional Item 2Michelle paints a wall that is 61/4 feet high and 623/4feet long. How many square feet does he paint?
i. 3723/16square feetii. 3921/2square feetiii. 3923/16 square feetiv. 3933/4square feet
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.

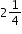
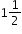 loaves for the French toast, how much bread does she have left?
loaves for the French toast, how much bread does she have left?