General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 5
Strand: Number Sense and Operations
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- NA
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to use place value understanding to plot, order and compare multi-digit numbers with decimals to the thousandths. In grade 4 (MA.4.NSO.1.5), decimals were plotted to the hundredths, and in grade 6 (MA.6.NSO.1.1) rational numbers, including negative numbers, will be plotted.- During instruction, students should apply understanding of flexible representations from MA.5.NSO.1.3 to help them reason while plotting, ordering and comparing.
- During instruction, teachers should show students how to represent these decimals on scaled number lines. Students should use place value understanding to make comparisons.
- Instruction expects students to justify their arguments when plotting, comparing and ordering (MTR.4.1).
Common Misconceptions or Errors
- Students may be confused when comparing numbers that have the same digits (but different values).
- For example, when comparing 2.459 and 13.24, a student may not consider the magnitude of the numbers and only look at their digits. That student may claim that 2.459 is greater than 13.24 because the digit 2 is greater than the digit 1 (though they are actually comparing 2 and 10).
Strategies to Support Tiered Instruction
- Instruction includes the use of place value charts, number lines and relational symbols to compare numbers to the thousandths that have the same amount of digits but different values. It is imperative for students to develop a conceptual understanding of rounding, such as what the benchmarks are, using place value understanding to round numbers without instruction of mnemonics, rhymes or songs.
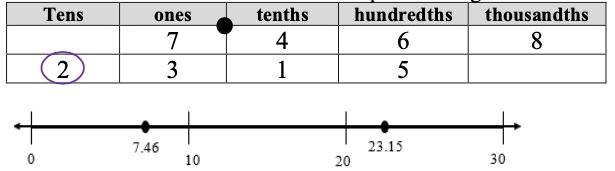
- For example, when comparing 7.468 and 23.15, students record 7.468 and 23.15 in a place value chart. The teacher asks students to compare these numbers, beginning with the greatest place value and explains that the number 23.15 has 2 tens and the number 7.468 does not have any tens so 7.468 < 23.15 and 23.15 > 7.468 even though both numbers have the same amount of digits. Also, students plot 7.468 and 23.15 on a number line to compare the magnitude of the numbers.
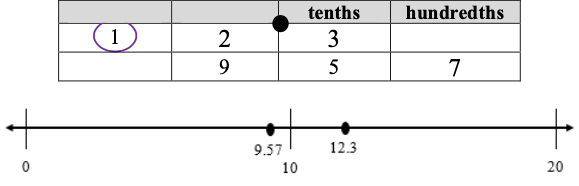
- For example, when comparing 12.3 and 9.57 students record 12.3 and 9.57 in a place value chart. The teacher asks students to compare these numbers, beginning with the greatest place value while explaining that the number 12.3 has one ten and the number 9.57 does not have any tens so 9.57 < 12.3 and 12.3 > 9.57 even though both numbers have the same amount of digits. Also, students plot 12.3 and 9.57 on a number line to compare the magnitude of the numbers.
Instructional Tasks
Instructional Task 1 (MTR.3.1)
- Part A. Plot the numbers 1.519, 1.9, 1.409 and 1.59 on the number line below.
- Part B. Choose two values from the list and compare them using >, < or =.
- Part C. Choose a number between 1.519 and 1.59 and plot it on the number line.
- Part D. Use evidence from your number line to justify which number is greatest.
Instructional Items
Instructional Item 1
Select all the statements that are true.- a. 13.049 < 13.49
- b. 13.049 < 13.05
- c. 2.999 > 28.99
- d. 1.28 < 1.31
- e. 5.800 = 5.8
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.