Standard #: MA.4.AR.3.1


This document was generated on CPALMS - www.cpalms.org



Determine factor pairs for a whole number from 0 to 144. Determine whether a whole number from 0 to 144 is prime, composite or neither.


Clarifications


Clarification 1: Instruction includes the connection to the relationship between multiplication and division and patterns with divisibility rules.

Clarification 2: The numbers 0 and 1 are neither prime nor composite.



General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 4
Strand: Algebraic Reasoning
Standard: Recognize numerical patterns, including patterns that follow a given rule.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

Terms from the K-12 Glossary

  • Composite Number 
  • Factors 
  • Prime Number

Vertical Alignment

Previous Benchmarks

Next Benchmarks

Purpose and Instructional Strategies

The purpose of this benchmark is for students to begin understanding factors of whole numbers which sets the foundation for determining prime factorization in grade 6 (MA.6.NSO.3.4). 
  • This benchmark also refers to prime and composite numbers. Prime numbers have exactly two factors, the number one and the number itself (e.g., the number 13 has the factors of 1 and 13 only so it is a prime number). Composite numbers have more than two factors.
    • For example, 14 has the factors of 1, 2, 7 and 14. Since this number has more factors than 1 and 14, it is a composite number. 
  • Instruction may allow students to use divisibility rules to determine the factors of a number. 
    • All numbers are divisible by 1. 
    • All even numbers are divisible by 2. 
    • A number is divisible by 3 if the sum of the digits is divisible by 3. 
    • A number is divisible by 4 if the 2-digit number in the tens and ones places is divisible by 4. 
    • A number is divisible by 5 if the number in the ones place is a 0 or 5. 
    • A number is divisible by 6 if it is an even number and the sum of the digits is divisible by 3. 
    • A number is divisible by 9 if the sum of the digits is divisible by 9. 
  • Students should use models (arrays) to determine why a number would be prime or composite.

Common Misconceptions or Errors

  • Students may think of the number 1 as a prime number. It is neither prime nor composite. 
  • Students may also think that all odd numbers are prime. 
  • Some students may think that larger numbers have more factors. Have students share all factor pairs and how they found the factors.

Strategies to Support Tiered Instruction

  • Instruction includes opportunities to identify the factor pairs of whole numbers from 0- 144 with teacher guidance. Students also determine if the number is prime, composite or neither. The teacher refers to the divisibility rules shown above in “Purpose and Instructional Strategies” to support students as they determine the factors of the given number. Students use manipulatives and models (e.g., counters and arrays) to identify factors of the given number. 
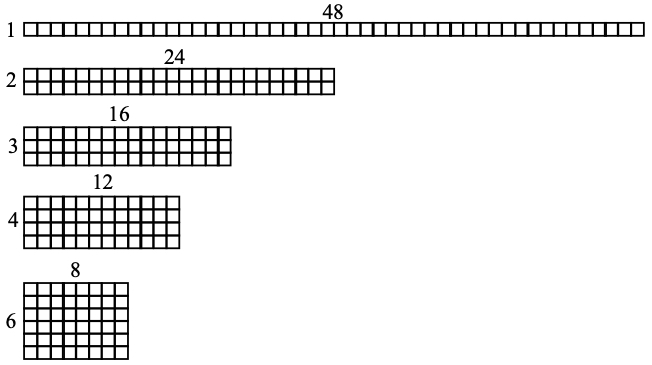
  • For example, the teacher displays the following number: 48. Students draw arrays to determine the factors of 48 (1, 2, 3, 4, 6, 8, 12, 16, 24, 48). Students may use multiplication and skip counting to check factor pairs (e.g., 5 can be ruled out as a factor because 5 × 9 = 45 and 5 × 10 = 50). The teacher asks students if 48 is prime, composite, or neither (composite). This is repeated with additional whole numbers from 0-144. 
Arrays
  • For example, the teacher displays the following number: 32. Students are provided 32 counters and use them to create arrays to determine the factors of 32 (1, 2, 4, 8, 16, 32). Students may use multiplication and skip counting to check factor pairs (e.g., 5 can be ruled out as a factor because 5 × 6 = 30 and 5 × 7 = 35). Students may explore using counters to rule out additional numbers as factors (e.g., if you make 6 rows with a total of 32 counters, there will not be an even number in each row). The teacher asks students if 32 is prime, composite, or neither (composite). This is repeated with additional whole numbers from 0- 144.
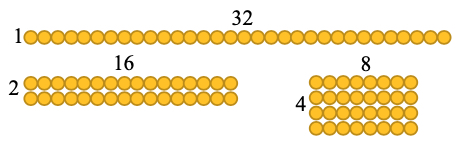
counters

Instructional Tasks

Instructional Task 1 (MTR.3.1) 

Find all the factors for the numbers between 20 and 30. What is the greatest prime number in this set of primes? What is the least prime number in this set of primes?

Instructional Items

Instructional Item 1 

Select all the statements are true about the number 84.
  • a. 42 is a factor of 84. 
  • b. 84 is a composite number. 
  • c. 84 has exactly 4 distinct factor pairs.  
  • d. The prime factors of 84 are 2, 6 and 7. 
  • e. 84 can be written as the product 2 × 2 × 3 × 7. 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.



Related Courses

Course Number1111 Course Title222
5012060: Grade Four Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7712050: Access Mathematics Grade 4 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current))
5012055: Grade 3 Accelerated Mathematics (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))
5012015: Foundational Skills in Mathematics 3-5 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.4.AR.3.AP.1 Explore factor pairs for a whole number. Factors may not exceed single-digit whole numbers.


Related Resources

Educational Games

Name Description
Arithmetic Workout

This tutorial will help you to brush up on your multiplication, division and factoring skills with this exciting game. 

Sigma Prime: A Prime Factorization Game


This fun and engaging game will test your knowledge of whole numbers as prime or composite.  As you shoot the asteroids with a particular factor, the asteroids will break down by that chosen factor.  Keep shooting the correct factors to totally eliminate the asteroids.  But be careful, shooting the wrong factor has consequences!

Formative Assessments

Name Description
Find All the Factor Pairs

Students are asked to find all the factor pairs for each of four given numbers.

Factor Pairs

Students are asked to find all the factor pairs of a given number and identify the number as a multiple of the factors.

Prime or Composite

Students are asked to determine whether each of four given numbers is prime or composite and justify their choices.

Lesson Plans

Name Description
Divisibility Rules and Factors

The students will determine divisibility rules by looking for a pattern in multiples of a number. They will then utilize divisibility rules to find factors thereby strengthening this ability. The students will practice their factoring skills through the Four in a Row game. This lesson could be an introduction to divisibility rules but not findng factors.

Fantastic Factors

In this lesson, students will start out using manipulatives to create arrays which will be used to find factor pairs. Students will use a T-Chart to determine the factor pairs of numbers. Students will then use their T-Charts to determine if a number is prime or composite.

Hooray for arrays!

Students will identify prime and composite numbers through arrays. The lesson begins with a fun situational story.

Abundant Numbers

This lesson provides practice in learning factors of numbers. Students will play a factor game then participate in a thought-provoking task. It is helpful if students know what a prime number is, but it is not essential.

Using Rectangles to Find Prime and Composite Numbers

In this lesson, students will be using rectangles to find prime and composite numbers.  Students will draw different rectangles for the area of a given set of numbers.  They will determine the factor pairs for each number in the given set and use them to discover the meaning of prime and composite numbers.

Factor That!

This is a foundation lesson in which the students will visually see the relationship between factors and products. As a result of this hands-on lesson and guided discussion, they will learn to identify the factors of a given number.

Numbers Grow Here

The students will use prior knowledge of the area formula to design a garden with a  area. Students will compare gardens and note that rectangles with the same area could have different dimensions.

Factor Word Challenges

Students will apply multiplication, division and factor knowledge to word problems.

Fun with Factors

This is an introductory lesson addressing factors for number 1-20. Factoring will lead students to discover differences and similarities between prime and composite numbers. Students will also discuss five claims about factors, prime, and composite numbers and create support from examples and non-examples to determine whether these claims are valid or invalid.

Searching for the Primes

Students will use a 100s chart to sort out the prime numbers under 100 using the Sieve of Eratosthenes method. 

Prime Factorization - From Fingerprints to Factorprints

This activity provides an introduction to composite numbers and prime numbers through factorization.

Area and Perimeter of Rectangles Investigations

Students will determine the validity of the statement, "All rectangles with the same area will have the same perimeter" through two investigations.

Original Student Tutorial

Name Description
Prime and Composite Backyard Dilemma

Discover what makes prime and composite numbers unique thanks to an interesting backyard problem in this interactive tutorial.

Problem-Solving Task

Name Description
Identifying Multiples

The goal of this task is to work on finding multiples of some whole numbers on a multiplication grid. After shading in the multiples of 2, 3, and 4 on the table, students will see a key difference.  The focus can be on identifying patterns or this can be an introduction or review of prime and composite numbers.

Tutorial

Name Description
Recognizing Prime and Composite Numbers

This Khan Academy tutorial video reviews how to determine if a number is prime or composite.

Student Resources

Original Student Tutorial

Name Description
Prime and Composite Backyard Dilemma :

Discover what makes prime and composite numbers unique thanks to an interesting backyard problem in this interactive tutorial.

Educational Games

Name Description
Arithmetic Workout:

This tutorial will help you to brush up on your multiplication, division and factoring skills with this exciting game. 

Sigma Prime: A Prime Factorization Game:


This fun and engaging game will test your knowledge of whole numbers as prime or composite.  As you shoot the asteroids with a particular factor, the asteroids will break down by that chosen factor.  Keep shooting the correct factors to totally eliminate the asteroids.  But be careful, shooting the wrong factor has consequences!

Problem-Solving Task

Name Description
Identifying Multiples:

The goal of this task is to work on finding multiples of some whole numbers on a multiplication grid. After shading in the multiples of 2, 3, and 4 on the table, students will see a key difference.  The focus can be on identifying patterns or this can be an introduction or review of prime and composite numbers.

Tutorial

Name Description
Recognizing Prime and Composite Numbers:

This Khan Academy tutorial video reviews how to determine if a number is prime or composite.



Parent Resources

Problem-Solving Task

Name Description
Identifying Multiples:

The goal of this task is to work on finding multiples of some whole numbers on a multiplication grid. After shading in the multiples of 2, 3, and 4 on the table, students will see a key difference.  The focus can be on identifying patterns or this can be an introduction or review of prime and composite numbers.



Printed On:5/3/2025 10:14:12 AM
Print Page | Close this window