General Information
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Equation
- Expression
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
- Contexts involving multiplying whole numbers and fractions lend themselves to modeling and examining patterns.
- This benchmark builds on students’ work of adding fractions with like denominators (MA.4.FR.2.2) and extending that work into the relationship between addition and multiplication.
- Students should use fraction models and drawings to show their understanding. Fraction models may include area models, number lines, set models, or equations.
- During instruction, teachers should relate “ total group size” language that was used to introduce whole number multiplication- possibly changing from “ total group size” to “ total size” or “ total amount” (see Appendix A). Using such language, the expression
5 × can be described as the total size or amount of 5 objects, each of which has size or amount of .
- For example, the weight of 5 slabs of chocolate that each weigh of a pound is 5 × pounds. Students need to understand that when multiplying a whole number by a fraction, the most important idea is that the whole number describes the number of objects and the fraction describes the size of each object.
- Instruction should include representing a whole number times a fraction as repeated addition: 5× = + + + +
- When multiplying a fraction by a whole number, teachers can use language like “portion of” to convey that the fraction represents the “portion of” the whole number.
- For example, the portion of a 5 mile run is × 5 miles.
- Instruction includes fractions equal to and greater than one.
- Exploring patterns of what happens to the numerator when a whole number is multiplied by a fraction will help students make sense of multiplying fractions by fractions in Grade 5. When multiplying whole numbers by mixed numbers, students can use the distributive property or write the mixed number as a fraction greater than one. During instruction, students should compare both strategies. Using the distributive property to multiply a whole number by a mixed number could look like this.
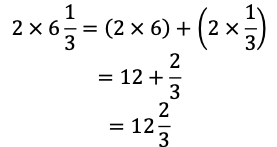
Common Misconceptions or Errors
- Students may multiply both the numerator and the denominator by the whole number. It is important to provide students with visual models, manipulatives or context to model the computation.
- Students may be confused by the fact that a fraction times a whole number often represents something quite different than a whole number times a fraction, even though the commutative property says the order does not affect the value.
- Without a conceptual understanding of how fraction multiplication is modeled, students can be confused regarding why the denominator remains the same when multiplying a whole number by a fraction. During instruction, teachers should relate fraction multiplication to repeated addition to explain why only the numerator changes.
Strategies to Support Tiered Instruction
- Instruction includes connecting repeated addition and models to understand the meaning of the factors in a multiplication equation.
- For example, 8 × can be shown using repeated addition with 8 groups of .
- + + + + + + + = or 2 wholes
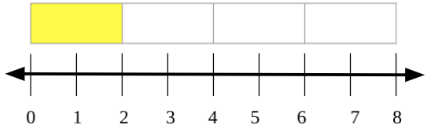
- For example, × 8 can be shown as of 8 using a number line.
- For example, 8 × can be shown using repeated addition with 8 groups of .
- Instruction includes real-world situations aligned with the content. The teacher provides a multiplication expression with real-world context and items to represent the situation to make connections.
- For example, the teacher provides the student with the following situation: “The theater class has to make costumes that require foot of ribbon. They need to make 8 costumes. How many feet of ribbon will they need total?” The teacher provides ribbon already cut into foot pieces and has students model the problem. Students then write out the repeated addition problem to match + + + + + + + = or 2 feet.
- For example, the teacher provides the student with the following situation: “The theater class has 8 feet of ribbon. They need to make 4 costumes and they want to use up all of the ribbon. How many feet of ribbon does each costume use?” The teacher will provide the student with a piece of ribbon 8 feet long and have them mark it off into 4 equal sections and find the length of 1 section (2 feet).
- Teacher provides models that represent multiplication expressions to represent the Commutative Property of Multiplication and has students explain the difference in meaning.
- For example, the teacher provides the student with the following models.
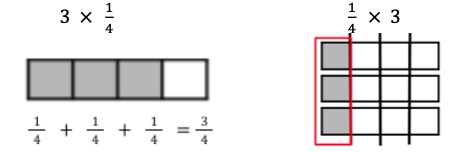
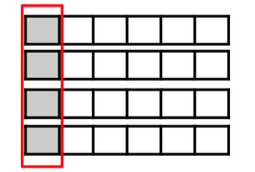
- The teacher provides models and asks students which expression it models.
- For example, the teacher provides students with the following model and asks if it represents x 4 or 4 x
Instructional Tasks
Instructional Task 1 (MTR.2.1)
How many are in ? Use a visual model to explain your reasoning and show the relationship to the multiplication of a whole number by a fraction.Instructional Items
Instructional Item 1
An expression is shown.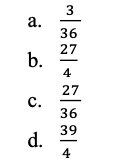
Instructional Item 2
Choose all the ways to express the product of × 5.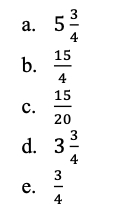

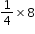 by imagining having 8 pizzas that she wants to split equally with three of her friends. She and each of her friends will get 2 pizzas since
by imagining having 8 pizzas that she wants to split equally with three of her friends. She and each of her friends will get 2 pizzas since 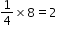 .
.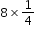 by imagining having 8 pizza boxes each with one-quarter slice of a pizza left. If she put them all together, she would have a total of 2 whole pizzas since
by imagining having 8 pizza boxes each with one-quarter slice of a pizza left. If she put them all together, she would have a total of 2 whole pizzas since 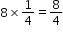 which is equivalent to 2.
which is equivalent to 2.
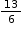 and record their work with an equation.
and record their work with an equation.