General Information
Subject Area: Mathematics (B.E.S.T.)
Grade: 3
Strand: Number Sense and Operations
Date Adopted or Revised: 08/20
Status: State Board Approved
Benchmark Instructional Guide
Connecting Benchmarks/Horizontal Alignment
Terms from the K-12 Glossary
- Equal sign
- Expression
- Equation
- Whole Number
Vertical Alignment
Previous Benchmarks
Next Benchmarks
Purpose and Instructional Strategies
The purpose of this benchmark is for students to add and subtract multi-digit whole numbers with procedural fluency. Students use skills from the procedural reliability stage in Grade 2 to become fluent with efficient and accurate procedures, including standard algorithms for addition and subtraction. In Grade 2, students added and subtracted multi-digit whole numbers up to 1,000. In Grade 3, the magnitude of numbers increases.- A standard algorithm is defined as any efficient and accurate procedure that allows students to add and subtract whole numbers. Students’ choices of standard algorithms for addition and subtraction do not need to be the same (MTR.5.1).
- Students should be able to justify their use of a standard algorithm for adding and subtracting by explaining the steps mathematically. Each student should be able to explain if and when regrouping is needed, and how regrouping is computed using their chosen algorithm. During instruction, teachers and students should work together to relate place value understanding to algorithms (MTR.3.1, MTR.4.1, MTR.5.1).
- Problems should include both vertical and horizontal forms, including opportunities for students to apply the commutative and associative properties.
- Instruction of this benchmark should be taught with MA.3.NSO.1.4. Students should use rounding as a means to estimate reasonable solutions of sums and differences before calculating (MTR.6.1).
Common Misconceptions or Errors
- Students who learn a standard algorithm without being able to explain why it works using place value understanding often make computational errors and/or cannot determine if their solutions are reasonable. To assist students with this misconception, students should justify the algorithm they choose by checking for reasonableness.
- Students who cannot explain their steps mathematically often have difficulty understanding regrouping. Many computational errors are a result of students not discovering this conceptual understanding while they practiced adding and subtracting with procedural reliability in Grade 2 (MA.2.NSO.2.3 and MA.2.NSO.2.4). Instruction that focuses on learning standard algorithms for addition and subtraction as a series of steps without checking for conceptual understanding will contribute to regrouping errors.
Strategies to Support Tiered Instruction
- Instruction includes guiding students through the process of estimating reasonable values for sums and differences using an understanding of place value, addition, and subtraction.
- For example, students make reasonable estimates for the sum of 174 + 253. Instruction includes a prompt such as “Before using an algorithm, we will estimate the sum to make sure that we are using the algorithm correctly and our answer is reasonable. The first addend of 174 is close to the benchmark number 200 and the second addend of 253 is close to the benchmark number 250. So, we can use 200 + 250 = 450 to estimate that our sum should be close to 450.”
- Instruction includes guiding students through the process of explaining and justifying the chosen algorithm and determining if an algorithm was used correctly by reviewing the reasonableness of solutions.
- For example, students use a standard algorithm to solve 174 + 253 and explain their thinking using a place value visual representation. Instruction includes a prompt such as “Begin by adding in the one's place. 4 ones plus 3 ones is 7 ones. Because the total number of ones is less than 10, it is not necessary to regroup. Next, add in the tens place. 7 tens plus 5 tens is 12 tens. Because I have more than 10 tens it is necessary to regroup the 10 tens to make one hundred. After composing a group of 10 tens there are 2 tens remaining. Finally, add 1 hundred plus 2 hundreds. Add the 1 hundred that was regrouped from the tens place. The sum is 427. Our sum of 427 is close to our estimate of 450, this helps us determine that our answer is reasonable”
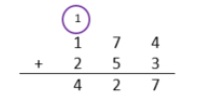
- For example, students use a standard algorithm to solve 327 − 174 and explain their thinking using a place value visual representation. Instruction includes prompts such as “ Begin subtracting 174 starting in the one's place. 7 ones minus 4 ones are 3 ones. There are not enough tens to subtract 7 tens from 2 tens. It is necessary to decompose one hundred into 10 tens. Now there are 12 tens, and there is enough to subtract 7 tens. 12 tens minus 7 tens equals 5 tens. Finally, subtract the hundreds: 3 hundreds minus 1 hundred equals 2 hundreds. The difference is 253.”
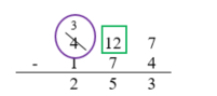
- For example, students use a standard algorithm and base-ten blocks to solve 62 − 37 and explain their thinking using a place value visual representation. Instruction includes a prompt such as “Begin subtracting 37 starting in the one's place. There are not enough ones to subtract 7 ones from 2 ones. It is necessary to decompose one ten into 10 ones. Now there are 12 ones and there is enough to subtract 7 ones. 12 ones take away 7 ones equals 5 ones. Finally, subtract the tens: 5 tens minus 3 tens is 2 tens. The difference is 25.”
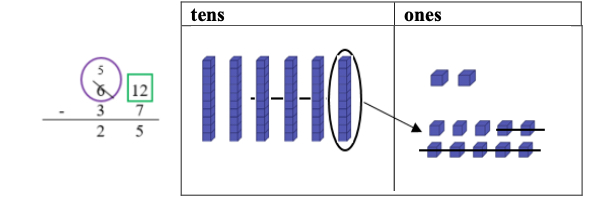
- Teacher provides guidance on using strategies based on place value to add and subtract.
- For example, students use strategies based on place value to solve 174 + 253. Students can decompose each number into expanded form, then add each place value separately (add the ones together, the tens together, and the hundreds together). Then, students can add together the sums of the ones, tens and hundreds to compute the sum.
Instructional Tasks
Instructional Task 1 (MTR.3.1, MTR.7.1)
- Miranda finds 492 seashells during her vacation. She now has 1,045 seashells in her collection. How many seashells did she have in her collection before vacation?
- Part A. Solve using a standard algorithm.
- Part B. Indicate one step where you needed to regroup while solving and show how you did it using words or a pictorial model.
- Mount Pleasant Elementary School had a penny fundraiser last week to raise money for families that were affected by the recent storm. The chart below shows how many pennies they raised each day.
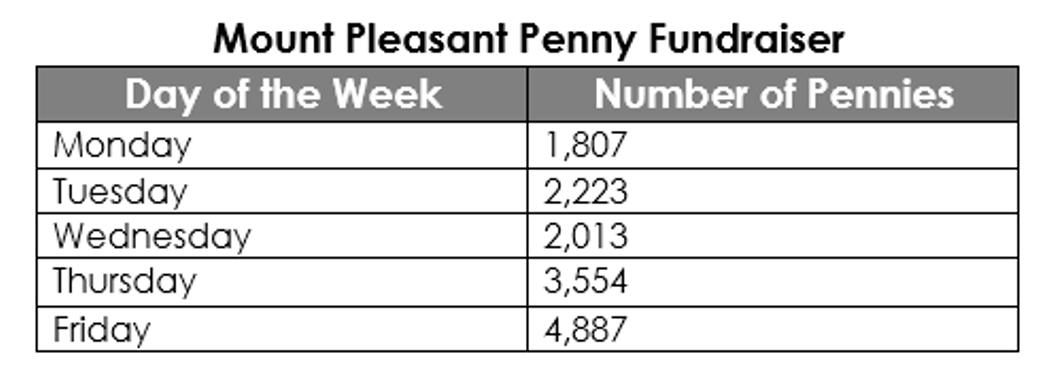
- Part A. How many more pennies were collected on Monday and Tuesday than on Thursday?
- Part B. Mrs. William’s class collected 1,627 of Friday’s total pennies. How many pennies did the rest of the school collect on Friday?
- Part C. The principal said the school collected about 6,000 pennies on Monday, Tuesday and Wednesday. Is this a reasonable estimate? Explain how you know.
2,558 + 2,677 = ?
- Part A. Write a word problem using the equation shown above.
- Part B. Solve the word problem you created in two different ways. Explain your thinking.
- Maya downloaded 856 songs to her music library last month. This month, she downloaded 726 more songs. Then, she deleted 119 songs that she no longer liked.
- Part A. How many songs does Maya have in her music library now?
- Part B. How many more songs will Maya need to download before she has 3,000 songs in her music library?
- Part C. What are two different ways you could solve this problem? Show your thinking.
- Shay wants to find the sum of 2,417 and 3,568. Explain the steps for finding the sum of 2,417 and 3,568. Be sure to include the words thousands, hundreds, tens, ones, and sum in your explanation.
Instructional Items
Instructional Item 1
- What is the sum of 1,432 and 2,981?
Instructional Item 2
- What is the difference of 8,000 and 1,432?
Instructional Item 3
- Cameron set a goal of collecting 7,000 stickers this year. In January, he collected 895 stickers, in February, he collected 472 stickers, and in March he collected 927 stickers. How many more stickers does he need to collect to meet his goal for the year?
- Use rounding to estimate the sum of 4,587 and 926. Then, find the actual sum of the two numbers.
*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.