Standard #: MA.2.AR.1.1


This document was generated on CPALMS - www.cpalms.org



Solve one- and two-step addition and subtraction real-world problems.


Clarifications


Clarification 1: Instruction includes understanding the context of the problem, as well as the quantities within the problem.

Clarification 2: Problems include creating real-world situations based on an equation.

Clarification 3: Addition and subtraction are limited to sums up to 100 and related differences. Refer to Situations Involving Operations with Numbers (Appendix A).



General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 2
Strand: Algebraic Reasoning
Standard: Solve addition problems with sums between 0 and 100 and related subtraction problems.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Associative Property of Addition 
  • Commutative Property of Addition 
  • Equation 
  • Expression
  • Number line

 

Vertical Alignment

Previous Benchmarks

 

Next Benchmarks

 

 

Purpose and Instructional Strategies

The purpose of this benchmark is to provide opportunities for students to solve various real-world situation types involving addition and subtraction. In grade 1, students solved real-world addition and subtraction problems within 20 (MTR.7.1). 
  • Instruction includes experience with all situation types involving addition and subtraction. 
  • Mastery of all situation types, as shown in Appendix A, is expected at by the end of this grade level. 
  • Instruction leads students to focus on context and apply reasoning to determine the appropriate operation. 
  • Instruction includes the use of number lines, drawings, diagrams or models to represent problem context.

 

Common Misconceptions or Errors

  • Students may have difficulty interpreting the quantities in the context of the problem or misidentifying the operation needed to solve the problem. 
  • Students may interpret a start or change unknown problem as a result unknown problem.
  • Students may look for key words which can lead to the wrong operation and cause students to ignore context and reasoning.

 

Strategies to Support Tiered Instruction

  • Teacher provides a graphic organizer to record information about the problem that focuses on the quantities in context and the operation(s) needed to solve the problem. 
  • For example, use the following problem to complete the organizer below. 
    • John collected 23 leaves on his walk on Monday. On Tuesday, he collected 35 leaves on his walk. At the end of his walk on Wednesday, he had collected a total of 97 leaves. How many leaves did he collect on Wednesday? 
    • What is this problem about? John collected leaves on Monday, Tuesday, and Wednesday. 
    • What do I know? John collected 23 leaves on Monday and 35 leaves on Tuesday. He has a total of 97 leaves. 
    • What is the problem asking? How many leaves did John collect Wednesday? 
    • Does this problem have one or two steps? This problem has 2 steps.
    • What operation can I use to solve this problem? I can add and subtract.
    • How can I model this problem to solve it? Students may use an equation, a drawing, or manipulatives to model their work. 

  • Teacher provides the chart/organizer below and guides students through determining if the start, change and result are known for each problem.
    • Example: 

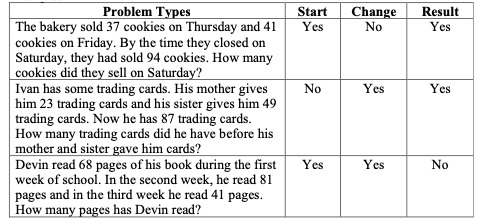
  • Instruction provides opportunities to determine the context of numberless word problems with a focus on what is happening in the problem and how to solve it. 
    • For example, the teacher provides the following word problem to students. Cindy Lou needs ___ cupcakes for the bake sale. She has already made ___ cupcakes. How many cupcakes does she still need to make? Teacher asks: What is this problem about? What is happening in this problem? What information do we know? How do you think you would solve this problem?

 

Instructional Tasks

Instructional Task 1(MTR.4.1) 

A bus leaves Park Elementary School with 27 students. Twelve students get off at stop A and eight more get off at stop B. How many students are on the bus at stop C? [Teacher note: Discussion of student responses should allow the opportunity to make connections between varying strategies and discuss the efficiency of a chosen strategy.]

Instructional Task 2
Create a word problem that can be solved using the equation 76=11+65.

Instructional Items

Instructional Item 1 

Mr. Gene sharpened some pencils. Ms. Smith sharpened 32 pencils. There are 78 sharpened pencils. How many pencils did Mr. Gene sharpen?

Instructional Item 2

Josephine bought 86 tickets at the fair to go on rides. She used 28 tickets for rides. She then gave her sister 11 tickets so she could ride some rides too. How many tickets does Josephine have left?

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.




Related Courses

Course Number1111 Course Title222
5012040: Grade Two Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7712030: Access Mathematics Grade 2 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current))
5012005: Foundational Skills in Mathematics K-2 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.2.AR.1.AP.1 Determine if addition or subtraction equations with no more than three terms are true or false. Sums may not exceed 20 and their related subtraction facts.


Related Resources

Formative Assessments

Name Description
Compare (Bigger Unknown) Word Problems

Students are asked to solve two Compare (Bigger Unknown) word problems: one involving the word more and one involving the word fewer.

Solving a Two-Step Word Problem: Eating Grapes

Students are asked to solve a two-step word problem that combines a Compare (Bigger Unknown) problem and a Compare (Smaller Unknown) problem.

Compare (Smaller Unknown) Word Problems

Students are asked to solve two Compare (Smaller Unknown) word problems: one involving the word more and one involving the word fewer.

Solving a Two-Step Word Problem: Marbles in a Bag

Students are asked to solve a two-step word problem that combines a Put Together (Result Unknown) problem and a Take From (Result Unknown) problem.

Word Problems with Result Unknown

Students are asked to solve three word problems: Add To (Result Unknown), Take From (Result Unknown), and Put Together/Take Apart (Total Unknown).

Solving a Two-Step Word Problem: Going Fishing

Students are asked to solve a two-step word problem that combines an Add To (Result Unknown) problem and a Compare (Difference Unknown) problem.

One, Two, Three Problems to Solve

Students are asked to solve three word problems: Put Together (Addend Unknown), Take From (Change Unknown), Add to (Change Unknown).

How Many More and How Many Fewer?

Students are asked to solve two Compare (Difference Unknown) word problems: a how many more and a how many fewer variation.

Both Addends Unknown

Students are asked to solve a Put Together/Take Apart (Both Addends Unknown) word problem and explain their strategies.

Add To and Take From (Start Unknown)

Students are asked to solve two word problems: Add To (Start Unknown) and Take From (Start Unknown).

Lesson Plans

Name Description
Word Problems Galore!

This lesson contains multiple word problems from various situation types. Different numbers for each problem are given based on student need.

How Much Do We Need to Order?

Students are provided the task of determining the total number of students in Kindergarten, first, and second grades in their school. Students will develop a plan to collect the information. Students will create a table to represent the data and find the total number of students.

Sweet Donut Shop

In this Model Eliciting Activity, MEA, students will help the Sweet Donut Shop determine what the newest donut will be. Students are given the cost to make each batch along with the selling price and are asked to determine the profit for each batch. Students create a procedure for ranking the donuts and write a letter explaining the procedure and the ranking. In the “twist” students are provided the starting and finishing times for each batch. They must determine the total amount of time, decide if their procedure should change based on the new information, and write a letter explaining whether the procedure changed and the new ranking of the donuts.

Model Eliciting Activities, MEAs, are open-ended, interdisciplinary problem-solving activities that are meant to reveal students’ thinking about the concepts embedded in realistic situations. MEAs resemble engineering problems and encourage students to create solutions in the form of mathematical and scientific models. Students work in teams to apply their knowledge of science and mathematics to solve an open-ended problem, while considering constraints and tradeoffs. Students integrate their ELA skills into MEAs as they are asked to clearly document their thought process. MEAs follow a problem-based, student centered approach to learning, where students are encouraged to grapple with the problem while the teacher acts as a facilitator. To learn more about MEA’s visit: https://www.cpalms.org/cpalms/mea.aspx

Words and Subtraction

In this lesson, students will build on their earlier work of representing and solving situational problems (result unknown, change unknown, start unknown). Students will use related equations or drawings.

Let's Do Some Solving

In this lesson students will solve one-step addition word problems using base ten blocks, hundred charts, drawings, or strategies based on place value and/or the relationship between addition and subtraction.

Roll and Add Two Digit Numbers

In this lesson students will use two dice to roll and add two-digit numbers. Students will also use their numbers to create and solve one-step addition word problems.

Success with Story Problems - Addition/Subtraction

In this lesson, students will solve one and two-step real-world problems using a variety of problem-solving strategies.

Sweet Addition and Subtraction

This lesson is a continuation of the "Sweet Values" and "Sweet Number Places" lessons also found on CPALMS. It is a different way of teaching addition and subtraction, by continuing a story that started with place value. In this lesson, students will learn to use the place value knowledge gained to solve word problems.

Problem-Solving Task

Name Description
School Supplies

This task could be used for either instructional or assessment purposes, depending on where students are in their understanding of addition and how the teacher supports them. The solution shown is very terse; students' solution strategies are likely to be much more varied.

Tutorials

Name Description
Repeated Addition Example

In this tutorial you will learn how to solve a word problem by creating a chart and adding the same number many times.

Solving word problems within 100

This Khan Academy tutorial, called, "sports on a die" explains the pitfalls of relying on key words in a word problem. Students solve a problem by writing a missing addend addition equation and solve with the standard algorithm for subtracting two digit numbers.

Subtracting within 100 using the standard algorithm

In this tutorial video from Khan Academy, called "Using crayons", explore subtracting within 100 using the standard algorithm, as well as a bar diagram.

Solving a word problem using the standard algorithm for subtraction

In this video tutorial from Khan Academy called "losing tennis balls", explore solving a two-step subtraction word problem using the standard algorithm.

Adding two-digit numbers using the standard algorithm

In this tutorial video from Khan Academy, called "Fence posts for horses", explore adding a two digit number to a two digit number using the standard algorithm

Adding and subtracting on number line word problems

In this video tutorial from Khan Academy, explore using a number line solve word problems involving more than two numbers.

Student Resources

Problem-Solving Task

Name Description
School Supplies:

This task could be used for either instructional or assessment purposes, depending on where students are in their understanding of addition and how the teacher supports them. The solution shown is very terse; students' solution strategies are likely to be much more varied.

Tutorials

Name Description
Repeated Addition Example:

In this tutorial you will learn how to solve a word problem by creating a chart and adding the same number many times.

Solving word problems within 100:

This Khan Academy tutorial, called, "sports on a die" explains the pitfalls of relying on key words in a word problem. Students solve a problem by writing a missing addend addition equation and solve with the standard algorithm for subtracting two digit numbers.

Subtracting within 100 using the standard algorithm:

In this tutorial video from Khan Academy, called "Using crayons", explore subtracting within 100 using the standard algorithm, as well as a bar diagram.

Solving a word problem using the standard algorithm for subtraction:

In this video tutorial from Khan Academy called "losing tennis balls", explore solving a two-step subtraction word problem using the standard algorithm.

Adding two-digit numbers using the standard algorithm:

In this tutorial video from Khan Academy, called "Fence posts for horses", explore adding a two digit number to a two digit number using the standard algorithm

Adding and subtracting on number line word problems:

In this video tutorial from Khan Academy, explore using a number line solve word problems involving more than two numbers.



Parent Resources

Problem-Solving Task

Name Description
School Supplies:

This task could be used for either instructional or assessment purposes, depending on where students are in their understanding of addition and how the teacher supports them. The solution shown is very terse; students' solution strategies are likely to be much more varied.

Tutorials

Name Description
Solving word problems within 100:

This Khan Academy tutorial, called, "sports on a die" explains the pitfalls of relying on key words in a word problem. Students solve a problem by writing a missing addend addition equation and solve with the standard algorithm for subtracting two digit numbers.

Subtracting within 100 using the standard algorithm:

In this tutorial video from Khan Academy, called "Using crayons", explore subtracting within 100 using the standard algorithm, as well as a bar diagram.

Solving a word problem using the standard algorithm for subtraction:

In this video tutorial from Khan Academy called "losing tennis balls", explore solving a two-step subtraction word problem using the standard algorithm.

Adding two-digit numbers using the standard algorithm:

In this tutorial video from Khan Academy, called "Fence posts for horses", explore adding a two digit number to a two digit number using the standard algorithm

Adding and subtracting on number line word problems:

In this video tutorial from Khan Academy, explore using a number line solve word problems involving more than two numbers.



Printed On:6/13/2025 9:27:10 AM
Print Page | Close this window