Standard #: MA.1.FR.1.1


This document was generated on CPALMS - www.cpalms.org



Partition circles and rectangles into two and four equal-sized parts. Name the parts of the whole using appropriate language including halves or fourths.


Clarifications


Clarification 1: This benchmark does not require writing the equal sized parts as a fraction with a numerator and denominator.

General Information

Subject Area: Mathematics (B.E.S.T.)
Grade: 1
Strand: Fractions
Standard: Develop an understanding of fractions by partitioning shapes into halves and fourths.
Date Adopted or Revised: 08/20
Status: State Board Approved

Benchmark Instructional Guide

Connecting Benchmarks/Horizontal Alignment

 

Terms from the K-12 Glossary

  • Circle 
  • Rectangle

 

Vertical Alignment

Previous Benchmarks

 

Next Benchmarks

 

Purpose and Instructional Strategies

The purpose of this benchmark is to introduce the initial idea of equal parts in the form of halves and fourths. While students are not expected to use a numerator or denominator, it is the first exposure for students to see circles and rectangles partitioned into two or four equal-sized parts which sets the stage for fractional understanding. In Kindergarten, students recognized how combining two equal-sized triangles can form a rectangle. Also in Kindergarten, students learned that whole numbers up to 10 could be broken apart into two other whole numbers (MTR.5.1).
  • Instruction includes the idea of part-whole relationships as supported by the model (MTR.5.1). 
  • Instruction includes naming the parts based on the number of equal parts that make the whole. 
  • Instruction includes partitioning rectangles in multiple ways, such as horizontal, vertical, and diagonal, to show halves or fourths. Depending on the type of rectangle that is being presented, it may not result in four equal parts (MTR.2.1).

 

Common Misconceptions or Errors

  • Students may have difficulty partitioning circles or rectangles into equal-sized parts; additional guided practice may be helpful in these cases. 
  • When a rectangle is divided into fourths using its diagonals students may have trouble seeing that all four parts are the same size. This should not be a point of contention, but it should be an opportunity to explain to students that they will get a deeper understanding of this in later grades.

 

Strategies to Support Tiered Instruction

  • Teacher models partitioning circles and rectangles into fourths using a geoboard to investigate equal-sized parts. 
    • Example: 

partitioning circles and rectangles into fourths using a geoboard

  • Teacher models folding rectangles and circles into halves and fourths to develop an understanding of equal sized parts. 
  • Instruction provides opportunities to investigate equal sized parts using paper squares divided into fourths on the diagonal. 
    • For example, teacher provides paper squares and demonstrates how to divide it into fourths on the diagonal. Discussion should be centered on recognizing parts that are equal by folding the paper over onto itself to show the parts are equal.

equal sized parts using paper squares divided into fourths on the diagonal

 

Instructional Tasks

Instructional Task 1 (MTR.2.1, MTR.4.1) 

Part A. Partition the circles and rectangles in different ways to show two equal parts. Name the parts of the whole.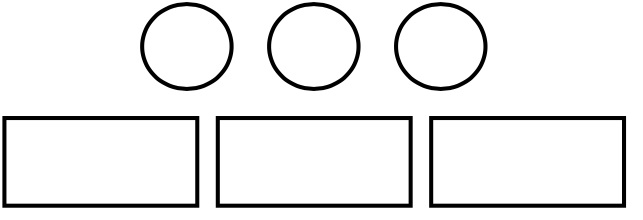 

  • My shapes are partitioned into ________________________. 
  • Compare with a partner to discuss if your circles and rectangles look alike and share how you know your shapes show two equal parts. 
Part B. Partition the circles and rectangles in different ways to show four equal parts. Name the parts of the whole. 

  • My shapes are partitioned into ________________________. 
  • Compare with a partner to discuss if your circles and rectangles look alike and share how you know your shapes show four equal parts. 

 

Instructional Task 2 (MTR.4.1) 

Josephine says she partitioned the clocks below into halves. Do you agree with her? Why or Why not? 

3 clocks

Enrichment Task 1 

Repeat Instructional Task 2 with halves replaced by fourths; helps makes the connection to grade 2.

 

Instructional Items

Instructional Item 1 

Divide a piece of paper into two parts so that each part has an equal amount. How could you describe each part? 

 

Instructional Item 2 

Pretend each of the circles below is a cake. 
  • The first one is for two people. Can you show how you would partition the cake for 2? This cake is partitioned into _________.
  • The second cake is for 4 people. Can you show how you would partition the cake for 4? This cake is partitioned into _________.

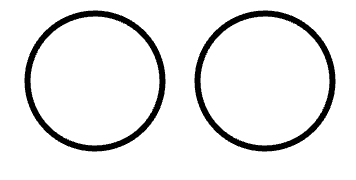
circles

 

*The strategies, tasks and items included in the B1G-M are examples and should not be considered comprehensive.



Related Courses

Course Number1111 Course Title222
5012030: Grade One Mathematics (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7712020: Access Mathematics Grade 1 (Specifically in versions: 2014 - 2015, 2015 - 2018, 2018 - 2022, 2022 and beyond (current))
5012005: Foundational Skills in Mathematics K-2 (Specifically in versions: 2019 - 2022, 2022 - 2024, 2024 and beyond (current))


Related Access Points

Access Point Number Access Point Title
MA.1.FR.1.AP.1 Partition circles and rectangles into two and four equal-sized parts. Recognize the parts of the whole as halves or fourths.


Related Resources

Formative Assessments

Name Description
Partition A Rectangle

Students partition a rectangle into two equal parts and then describe the parts.

Which Is Less?

Students are asked to share a rectangular cake between two people and then among four people and decide which results in smaller pieces.

Partition the Pizza

Students fold a picture of a circular pizza into four equal parts and then are asked to describe each part.

Half of a Rectangle

Students are asked to partition a rectangle into halves.

Lesson Plans

Name Description
It's a Piece of Cake...and Pizza

This lesson focuses only on partitioning circles and rectangles into two equal-sized parts, naming the parts with the word half/halves. Students will be partitioning paper pizzas and cakes to learn the concepts and then building pizzas through a game.

Equal Shares at the Zoo? Who Knew!

In this lesson, students will be partitioning shapes into halves and fourths. The class will get a letter from a zoo requesting their help in solving some problems with designing the layout of animal enclosures.

Halves and Quarters of Circles

In this lesson, students will learn how to partition circles into halves and quarters/fourths and examine how partitioning a circle into more equal shares creates smaller shares.

Pizza Anyone? Exploring Halves and Fourths/Quarters

This lesson practices the partitioning a whole to equal shares for halves, fourths, and quarters through pizza and candy bar manipulatives. Students are then challenged to demonstrate how many different ways they can fold a square sticky note into fourths!

Halves, Quarters and Fourths

In this lesson, the students will partition circles and rectangles into halves and fourths in order to gain a solid foundation for fractions.

Halves and Fourths

In this lesson, students will gain experience partitioning rectangle and circles into equal shares of halves and fourths and naming the parts appropriately.

Fair Share Picnic

In this introductory lesson on halves, pairs of students will rotate through math stations to prepare for a picnic. They will use paper materials to represent wholes and partition each whole into halves, using applicable mathematics vocabulary.

Halves and Fourths

This lesson uses a discovery approach to exploring the meaning of halves and fourths. The students will utilize math benchmarks as they analyze math solutions and explain their solutions. This lesson also teaches students that they can decompose larger sized parts to make smaller sized parts.

Halves and Wholes

In this lesson, students will gain a foundation for fractions by partitioning circles and rectangles into two equal-sized shares.

I'll Share With You

This lesson focuses on the beginning understanding of fractions through fair-sharing. Students will partition circles and rectangles into 2 and 4 equal-sized parts and be able to describe these parts using appropriate language such as halves and fourths.

A Fourth of That?

Students will partition circles and rectangles into four equal-sized parts. This is a foundational building block of fractions. Students should also develop an understanding of the idea of the whole. This is part of a series of lessons dealing with the foundation for fractions. The other two lessons are Resource ID 46582 and 46846. Throughout the three lessons the students are creating a Fraction Book.

Half of This, A Fourth of That, A Whole Lot of Fun!

Students will partition circles and rectangles into two and four equal-sized parts. They will also explore and discuss the concept that decomposing into more equal shares creates smaller shares. This is a foundational building block of fractions. Students should also develop an understanding of the idea of the whole. This is part of a series of lessons dealing with the foundation for fractions. The other two lessons are Resource IDs 46582 and 46764. Throughout the three lessons the students are creating a Fraction Book.

Half of This?

Students will partition circles and rectangles into two equal-sized parts. This is a foundational building block of fractions. Students should also develop an understanding of the idea of the whole. This is part of a series of lessons dealing with the foundation for fractions. The other two lessons are Resource ID 46764 and 46846. Throughout the three lessons the students are creating a Fraction Book.

Original Student Tutorials

Name Description
Equal Shares Heroes Find Fourths

Be a hero and partition circles and rectangles into four equal shares. Describe equal shares using the words "fourths" and "quarters" in this interactive tutorial.

Equal Shares Heroes

Help the heroes separate circles and rectangles into equal shares and describe the equal shares as "halves" or "half of" as you complete this interactive tutorial. 

Perspectives Video: Teaching Ideas

Name Description
Making Connections Between Partitioning Circles and Circle Graphs

Unlock an effective teaching strategy for connecting partitioning circles and circle graphs in this Teacher Perspectives video for educators.

One Handed Clocks

Unlock an effective teaching strategy for using one-handed clocks to help students learn to tell time in this Teacher Perspectives video for educators.

Problem-Solving Task

Name Description
Representing Half of a Rectangle

This task is for assessment purposes, providing a context for indentifying different ways of representing half of an object, a rectangle in this case. The task may also be used for instructional purposes but if so the teacher may wish to introduce some other ways of showing one half of the rectangle, such as dividing along a diagonal (and shading in one piece) or dividing it into four equal pieces, shading in two pieces that only touch at a corner.

Student Resources

Original Student Tutorials

Name Description
Equal Shares Heroes Find Fourths:

Be a hero and partition circles and rectangles into four equal shares. Describe equal shares using the words "fourths" and "quarters" in this interactive tutorial.

Equal Shares Heroes:

Help the heroes separate circles and rectangles into equal shares and describe the equal shares as "halves" or "half of" as you complete this interactive tutorial. 

Problem-Solving Task

Name Description
Representing Half of a Rectangle:

This task is for assessment purposes, providing a context for indentifying different ways of representing half of an object, a rectangle in this case. The task may also be used for instructional purposes but if so the teacher may wish to introduce some other ways of showing one half of the rectangle, such as dividing along a diagonal (and shading in one piece) or dividing it into four equal pieces, shading in two pieces that only touch at a corner.



Parent Resources

Problem-Solving Task

Name Description
Representing Half of a Rectangle:

This task is for assessment purposes, providing a context for indentifying different ways of representing half of an object, a rectangle in this case. The task may also be used for instructional purposes but if so the teacher may wish to introduce some other ways of showing one half of the rectangle, such as dividing along a diagonal (and shading in one piece) or dividing it into four equal pieces, shading in two pieces that only touch at a corner.



Printed On:5/24/2025 6:17:31 AM
Print Page | Close this window