This cluster includes the following access points.
Vetted resources educators can use to teach the concepts and skills in this topic.
| Name |
Description |
| I'm Focused on the Right Directrix: | In this lesson, the geometric definition of a parabola is introduced. Students will also learn how to write the equation of a parabola in vertex form given its focus and directrix. |
| Discovering Properties of Parabolas by Comparing and Contrasting Parabolic Equations: |
- Teachers can use this resource to teach students how to derive the equation of a parabola in vertex form y = a(x – h)2 + k, when given the (x, y) coordinates of the focus and the linear equation of the directrix.
- An additional interactive graphing spreadsheet can be used as a resource to aid teachers in providing examples.
|
| Acting Out A Parabola: the importance of a vertex and directrix: | Students will learn the significance of a parabola's vertex and directrix. They will learn the meaning of what exactly a parabola is by physically representing a parabola, vertex, and directrix. Students will be able to write an equation of a parabola given only a vertex and directrix. |
| Explore the Properties of a Parabola and Practice Writing its Equation: | Students learn parabola properties, how to write parabola equations, and how to apply parabolas to solve problems. |
| Definition of a Parabola: | Student will learn the algebraic representation of a parabola, given its focus and its directrix. |
| Ellipse Elements and Equations: | Students will write the equation of an ellipse given foci and directrices using graphic and analytic methods. |
| Anatomy of a Parabola: | Students learn the parts of a parabola and write its equation given the focus and directrix. A graphic organizer is used for students to label all parts of the parabola and how it is created. |
| Circle Reasoning: | Students use the Pythagorean Theorem (Distance Formula) to derive the Standard Equation of a Circle; then move between descriptions and equations of a circle. |
| Equations of Circles 1: | This lesson unit is intended to help you assess how well students are able to use the Pythagorean theorem to derive the equation of a circle and translate between the geometric features of circles and their equations. |
| Equations of Circles 2: | This lesson unit is intended to help you assess how well students are able to translate between the equations of circles and their geometric features and sketch a circle from its equation. |
| The Math Behind the Records: | Students will develop an understanding of how the position of the focus and directrix affect the shape of a parabola. They will also learn how to write the equation of a parabola given the focus and directrix. Ultimately this will lead to students being able to write an equation to model the parabolic path an athlete's center of mass follows during the high jump. |
| Run Fido, Run!: | A guided practice for deriving the equation of a circle and then identifying a location to tether a dog to maximize movement. |
| A Point and a Line to a Parabola!: | In this lesson, the student will use the definition of a parabola and a graphing grid (rectangular with circular grid imposed) to determine the graph of the parabola when given the directrix and focus. From this investigation, and using the standard form of the parabola, students will determine the equation of the parabola. |
| Introduction to the Conic Section Parabola: | This lesson is an introduction into conic sections using Styrofoam cups and then taking a closer look at the parabola by using patty paper to show students how a parabola is formed by a focus and a directrix. |
Vetted resources students can use to learn the concepts and skills in this topic.
Vetted resources caregivers can use to help students learn the concepts and skills in this topic.
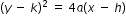or formula 
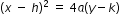for a parabola to write the equation when given the focus and directrix.