| Name |
Description |
| MA.912.AR.1.2: | Rearrange equations or formulas to isolate a quantity of interest.Clarifications:
Clarification 1: Instruction includes using formulas for temperature, perimeter, area and volume; using equations for linear (standard, slope-intercept and point-slope forms) and quadratic (standard, factored and vertex forms) functions. Clarification 2: Within the Mathematics for Data and Financial Literacy course, problem types focus on money and business.
|
Examples:
Algebra 1 Example: The Ideal Gas Law PV = nRT can be rearranged as 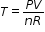 to isolate temperature as the quantity of interest. to isolate temperature as the quantity of interest. Example: Given the Compound Interest formula 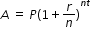 , solve for P. , solve for P. Mathematics for Data and Financial Literacy Honors Example: Given the Compound Interest formula 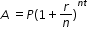 , solve for t. , solve for t.
|
|
| MA.912.AR.1.3: | Add, subtract and multiply polynomial expressions with rational number coefficients.Clarifications:
Clarification 1: Instruction includes an understanding that when any of these operations are performed with polynomials the result is also a polynomial.Clarification 2: Within the Algebra 1 course, polynomial expressions are limited to 3 or fewer terms.
|
|
| MA.912.AR.1.7: | Rewrite a polynomial expression as a product of polynomials over the real number system.Clarifications:
Clarification 1: Within the Algebra 1 course, polynomial expressions are limited to 4 or fewer terms with integer coefficients. |
|
| MA.912.AR.2.1: | Given a real-world context, write and solve one-variable multi-step linear equations. |
| MA.912.AR.2.2: | Write a linear two-variable equation to represent the relationship between two quantities from a graph, a written description or a table of values within a mathematical or real-world context.Clarifications:
Clarification 1: Instruction includes the use of standard form, slope-intercept form and point-slope form, and the conversion between these forms. |
|
| MA.912.AR.2.3: | Write a linear two-variable equation for a line that is parallel or perpendicular to a given line and goes through a given point.Clarifications:
Clarification 1: Instruction focuses on recognizing that perpendicular lines have slopes that when multiplied result in -1 and that parallel lines have slopes that are the same.
Clarification 2: Instruction includes representing a line with a pair of points on the coordinate plane or with an equation.
Clarification 3: Problems include cases where one variable has a coefficient of zero.
|
|
| MA.912.AR.2.4: | Given a table, equation or written description of a linear function, graph that function, and determine and interpret its key features.Clarifications:
Clarification 1: Key features are limited to domain, range, intercepts and rate of change. Clarification 2: Instruction includes the use of standard form, slope-intercept form and point-slope form. Clarification 3: Instruction includes cases where one variable has a coefficient of zero. Clarification 4: Instruction includes representing the domain and range with inequality notation, interval notation or set-builder notation. Clarification 5: Within the Algebra 1 course, notations for domain and range are limited to inequality and set-builder notations.
|
|
| MA.912.AR.2.5: | Solve and graph mathematical and real-world problems that are modeled with linear functions. Interpret key features and determine constraints in terms of the context.Clarifications:
Clarification 1: Key features are limited to domain, range, intercepts and rate of change.Clarification 2: Instruction includes the use of standard form, slope-intercept form and point-slope form. Clarification 3: Instruction includes representing the domain, range and constraints with inequality notation, interval notation or set-builder notation. Clarification 4: Within the Algebra 1 course, notations for domain, range and constraints are limited to inequality and set-builder. Clarification 5: Within the Mathematics for Data and Financial Literacy course, problem types focus on money and business.
|
Examples:
Algebra 1 Example: Lizzy’s mother uses the function C(p)=450+7.75p, where C(p) represents the total cost of a rental space and p is the number of people attending, to help budget Lizzy’s 16th birthday party. Lizzy’s mom wants to spend no more than $850 for the party. Graph the function in terms of the context. |
|
| MA.912.AR.2.6: | Given a mathematical or real-world context, write and solve one-variable linear inequalities, including compound inequalities. Represent solutions algebraically or graphically.
Examples:
Algebra 1 Example: The compound inequality 2x≤5x+1<4 is equivalent to -1≤3x and 5x<3, which is equivalent to
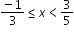 . . |
|
| MA.912.AR.3.1: | Given a mathematical or real-world context, write and solve one-variable quadratic equations over the real number system.Clarifications:
Clarification 1: Within the Algebra 1 course, instruction includes the concept of non-real answers, without determining non-real solutions.
Clarification 2: Within this benchmark, the expectation is to solve by factoring techniques, taking square roots, the quadratic formula and completing the square.
|
|
| MA.912.AR.3.4: | Write a quadratic function to represent the relationship between two quantities from a graph, a written description or a table of values within a mathematical or real-world context.Clarifications:
Clarification 1: Within the Algebra 1 course, a graph, written description or table of values must include the vertex and two points that are equidistant from the vertex.Clarification 2: Instruction includes the use of standard form, factored form and vertex form. Clarification 3: Within the Algebra 2 course, one of the given points must be the vertex or an x-intercept.
|
Examples:
Algebra I Example: Given the table of values below from a quadratic function, write an equation of that function.
x
| -2 | -1 | 0 | 1 | 2 | 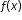
| 2 | -1 | -2 | -1 | 2 |
|
|
| MA.912.AR.3.5: | Given the x-intercepts and another point on the graph of a quadratic function, write the equation for the function. |
| MA.912.AR.3.6: | Given an expression or equation representing a quadratic function, determine the vertex and zeros and interpret them in terms of a real-world context. |
| MA.912.AR.3.7: | Given a table, equation or written description of a quadratic function, graph that function, and determine and interpret its key features.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; end behavior; vertex; and symmetry.Clarification 2: Instruction includes the use of standard form, factored form and vertex form, and sketching a graph using the zeros and vertex. Clarification 3: Instruction includes representing the domain and range with inequality notation, interval notation or set-builder notation. Clarification 4: Within the Algebra 1 course, notations for domain and range are limited to inequality and set-builder.
|
|
| MA.912.AR.3.8: | Solve and graph mathematical and real-world problems that are modeled with quadratic functions. Interpret key features and determine constraints in terms of the context.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; end behavior; vertex; and symmetry.Clarification 2: Instruction includes the use of standard form, factored form and vertex form. Clarification 3: Instruction includes representing the domain, range and constraints with inequality notation, interval notation or set-builder notation. Clarification 4: Within the Algebra 1 course, notations for domain, range and constraints are limited to inequality and set-builder.
|
Examples:
Algebra 1 Example: The value of a classic car produced in 1972 can be modeled by the function 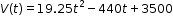 , where t is the number of years since 1972. In what year does the car’s value start to increase? , where t is the number of years since 1972. In what year does the car’s value start to increase? |
|
| MA.912.AR.4.1: | Given a mathematical or real-world context, write and solve one-variable absolute value equations. |
| MA.912.AR.4.2: | Given a mathematical or real-world context, write and solve one-variable absolute value inequalities. Represent solutions algebraically or graphically. |
| MA.912.AR.4.3: | Given a table, equation or written description of an absolute value function, graph that function and determine its key features.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; vertex; end behavior and symmetry. Clarification 2: Instruction includes representing the domain and range with inequality notation, interval notation or set-builder notation. Clarification 3: Within the Algebra 1 course, notations for domain and range are limited to inequality and set-builder.
|
|
| MA.912.AR.4.4: | Solve and graph mathematical and real-world problems that are modeled with absolute value functions. Interpret key features and determine constraints in terms of the context.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; vertex; end behavior and symmetry.Clarification 2: Instruction includes representing the domain, range and constraints with inequality notation, interval notation or set-builder notation.
|
|
| MA.912.AR.5.1: | Solve one-variable exponential equations using the properties of exponents. |
| MA.912.AR.5.2: | Solve one-variable equations involving logarithms or exponential expressions. Interpret solutions as viable in terms of the context and identify any extraneous solutions. |
| MA.912.AR.5.3: | Given a mathematical or real-world context, classify an exponential function as representing growth or decay.Clarifications:
Clarification 1: Within the Algebra 1 course, exponential functions are limited to the forms 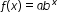 , where b is a whole number greater than 1 or a unit fraction, or , where b is a whole number greater than 1 or a unit fraction, or 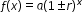 , where , where 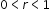 . .
|
|
| MA.912.AR.5.4: | Write an exponential function to represent a relationship between two quantities from a graph, a written description or a table of values within a mathematical or real-world context. |
| MA.912.AR.5.6: | Given a table, equation or written description of an exponential function, graph that function and determine its key features.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; constant percent rate of change; end behavior and asymptotes.
Clarification 2: Instruction includes representing the domain and range with inequality notation, interval notation or set-builder notation.
Clarification 3: Within the Algebra 1 course, notations for domain and range are limited to inequality and set-builder.
Clarification 4: Within the Algebra 1 course, exponential functions are limited to the forms
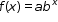 , where b is a whole number greater than 1 or a unit fraction or , where b is a whole number greater than 1 or a unit fraction or 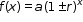 , where , where 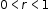 . . |
|
| MA.912.AR.5.7: | Solve and graph mathematical and real-world problems that are modeled with exponential functions. Interpret key features and determine constraints in terms of the context.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; constant percent rate of change; end behavior and asymptotes. Clarification 2: Instruction includes representing the domain, range and constraints with inequality notation, interval notation or set-builder notation. Clarification 3: Instruction includes understanding that when the logarithm of the dependent variable is taken and graphed, the exponential function will be transformed into a linear function. Clarification 4: Within the Mathematics for Data and Financial Literacy course, problem types focus on money and business.
|
Examples:
The graph of the function 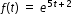 can be transformed into the straight line y=5t+2 by taking the natural logarithm of the function’s outputs. can be transformed into the straight line y=5t+2 by taking the natural logarithm of the function’s outputs. |
|
| MA.912.AR.5.8: | Given a table, equation or written description of a logarithmic function, graph that function and determine its key features.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; end behavior; and asymptotes.
Clarification 2: Instruction includes representing the domain and range with inequality notation, interval notation or set-builder notation.
|
|
| MA.912.AR.5.9: | Solve and graph mathematical and real-world problems that are modeled with logarithmic functions. Interpret key features and determine constraints in terms of the context.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; end behavior; and asymptotes.Clarification 2: Instruction includes representing the domain, range and constraints with inequality notation, interval notation or set-builder notation.
|
|
| MA.912.AR.6.1: | Given a mathematical or real-world context, when suitable factorization is possible, solve one-variable polynomial equations of degree 3 or higher over the real and complex number systems. |
| MA.912.AR.6.4: | Given a table, equation or written description of a polynomial function of degree 3 or higher, graph that function and determine its key features.Clarifications:
Clarification 1: Key features are limited to domain; range; intercepts; intervals where the function is increasing, decreasing, positive or negative; relative maximums and minimums; symmetry; and end behavior. Clarification 2: Instruction includes representing the domain and range with inequality notation, interval notation or set-builder notation.
|
|
| MA.912.AR.6.5: | Sketch a rough graph of a polynomial function of degree 3 or higher using zeros, multiplicity and knowledge of end behavior. |
| MA.912.AR.7.1: | Solve one-variable radical equations. Interpret solutions as viable in terms of context and identify any extraneous solutions. |
| MA.912.AR.8.1: | Write and solve one-variable rational equations. Interpret solutions as viable in terms of the context and identify any extraneous solutions.Clarifications:
Clarification 1: Within the Algebra 2 course, numerators and denominators are limited to linear and quadratic expressions. |
|
| MA.912.AR.9.1: | Given a mathematical or real-world context, write and solve a system of two-variable linear equations algebraically or graphically.Clarifications:
Clarification 1: Within this benchmark, the expectation is to solve systems using elimination, substitution and graphing.Clarification 2: Within the Algebra 1 course, the system is limited to two equations.
|
|
| MA.912.AR.9.4: | Graph the solution set of a system of two-variable linear inequalities.Clarifications:
Clarification 1: Instruction includes cases where one variable has a coefficient of zero.
Clarification 2: Within the Algebra 1 course, the system is limited to two inequalities.
|
|
| MA.912.AR.9.5: | Graph the solution set of a system of two-variable inequalities.Clarifications:
Clarification 1: Within the Algebra 2 course, two-variable inequalities are limited to linear and quadratic. |
|
| MA.912.AR.9.6: | Given a real-world context, represent constraints as systems of linear equations or inequalities. Interpret solutions to problems as viable or non-viable options.Clarifications:
Clarification 1: Instruction focuses on analyzing a given function that models a real-world situation and writing constraints that are represented as linear equations or linear inequalities. |
|
| MA.912.DP.2.4: | Fit a linear function to bivariate numerical data that suggests a linear association and interpret the slope and y-intercept of the model. Use the model to solve real-world problems in terms of the context of the data.Clarifications:
Clarification 1: Instruction includes fitting a linear function both informally and formally with the use of technology.Clarification 2: Problems include making a prediction or extrapolation, inside and outside the range of the data, based on the equation of the line of fit.
|
|
| MA.912.F.1.1: | Given an equation or graph that defines a function, determine the function type. Given an input-output table, determine a function type that could represent it.Clarifications:
Clarification 1: Within the Algebra 1 course, functions represented as tables are limited to linear, quadratic and exponential.
Clarification 2: Within the Algebra 1 course, functions represented as equations or graphs are limited to vertical or horizontal translations or reflections over the x-axis of the following parent functions:
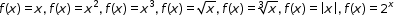 and and 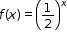 . . |
|
| MA.912.F.1.2: | Given a function represented in function notation, evaluate the function for an input in its domain. For a real-world context, interpret the output.Clarifications:
Clarification 1: Problems include simple functions in two-variables, such as f(x,y)=3x-2y. Clarification 2: Within the Algebra 1 course, functions are limited to one-variable such as f(x)=3x.
|
Examples:
Algebra 1 Example: The function 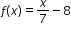 models Alicia’s position in miles relative to a water stand x minutes into a marathon. Evaluate and interpret for a quarter of an hour into the race. models Alicia’s position in miles relative to a water stand x minutes into a marathon. Evaluate and interpret for a quarter of an hour into the race. |
|
| MA.912.F.1.3: | Calculate and interpret the average rate of change of a real-world situation represented graphically, algebraically or in a table over a specified interval.Clarifications:
Clarification 1: Instruction includes making the connection to determining the slope of a particular line segment. |
|
| MA.912.F.1.9: | Determine whether a function is even, odd or neither when represented algebraically, graphically or in a table. |
| MA.912.F.2.1: | Identify the effect on the graph or table of a given function after replacing f(x) by f(x)+k,kf(x), f(kx) and f(x+k) for specific values of k.Clarifications:
Clarification 1: Within the Algebra 1 course, functions are limited to linear, quadratic and absolute value.Clarification 2: Instruction focuses on including positive and negative values for k.
|
|
| MA.912.F.2.2: | Identify the effect on the graph of a given function of two or more transformations defined by adding a real number to the x- or y- values or multiplying the x- or y- values by a real number. |
| MA.912.F.2.3: | Given the graph or table of f(x) and the graph or table of f(x)+k,kf(x), f(kx) and f(x+k), state the type of transformation and find the value of the real number k.Clarifications:
Clarification 1: Within the Algebra 1 course, functions are limited to linear, quadratic and absolute value. |
|
| MA.912.F.2.4: | Given the graph or table of values of two or more transformations of a function, state the type of transformation and find the values of the real number that defines the transformation. |
| MA.912.F.2.5: | Given a table, equation or graph that represents a function, create a corresponding table, equation or graph of the transformed function defined by adding a real number to the x- or y-values or multiplying the x- or y-values by a real number. |
| MA.912.F.3.4: | Represent the composition of two functions algebraically or in a table. Determine the domain and range of the composite function. |
| MA.912.F.3.5: | Solve mathematical and real-world problems involving composite functions. |
| MA.912.F.3.6: | Determine whether an inverse function exists by analyzing tables, graphs and equations. |
| MA.912.F.3.7: | Represent the inverse of a function algebraically, graphically or in a table. Use composition of functions to verify that one function is the inverse of the other.Clarifications:
Clarification 1: Instruction includes the understanding that a logarithmic function is the inverse of an exponential function. |
|
| MA.912.NSO.1.1: | Extend previous understanding of the Laws of Exponents to include rational exponents. Apply the Laws of Exponents to evaluate numerical expressions and generate equivalent numerical expressions involving rational exponents.Clarifications:
Clarification 1: Instruction includes the use of technology when appropriate.
Clarification 2: Refer to the K-12 Formulas (Appendix E) for the Laws of Exponents.
Clarification 3: Instruction includes converting between expressions involving rational exponents and expressions involving radicals.Clarification 4:Within the Mathematics for Data and Financial Literacy course, it is not the expectation to generate equivalent numerical expressions. |
|
| MA.912.NSO.1.2: | Generate equivalent algebraic expressions using the properties of exponents.
Examples:
The expression 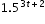 is equivalent to the expression is equivalent to the expression 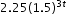 which is equivalent to which is equivalent to 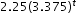 . . |
|
| MA.912.NSO.1.3: | Generate equivalent algebraic expressions involving radicals or rational exponents using the properties of exponents.Clarifications:
Clarification 1: Within the Algebra 2 course, radicands are limited to monomial algebraic expressions. |
|
| MA.912.NSO.1.4: | Apply previous understanding of operations with rational numbers to add, subtract, multiply and divide numerical radicals.Clarifications:
Clarification 1: Within the Algebra 1 course, expressions are limited to a single arithmetic operation involving two square roots or two cube roots. |
Examples:
Algebra 1 Example: The expression 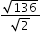 is equivalent to is equivalent to 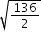 which is equivalent to which is equivalent to 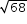 which is equivalent to which is equivalent to 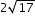 . . |
|
| MA.912.NSO.1.5: | Add, subtract, multiply and divide algebraic expressions involving radicals.Clarifications:
Clarification 1: Within the Algebra 2 course, radicands are limited to monomial algebraic expressions. |
|
| MA.912.NSO.1.6: | Given a numerical logarithmic expression, evaluate and generate equivalent numerical expressions using the properties of logarithms or exponents.Clarifications:
Clarification 1: Within the Mathematics for Data and Financial Literacy Honors course, problem types focus on money and business. |
|
| MA.912.NSO.1.7: | Given an algebraic logarithmic expression, generate an equivalent algebraic expression using the properties of logarithms or exponents.Clarifications:
Clarification 1: Within the Mathematics for Data and Financial Literacy Honors course, problem types focus on money and business. |
|
| MA.912.NSO.2.1: | Extend previous understanding of the real number system to include the complex number system. Add, subtract, multiply and divide complex numbers. |
| MA.K12.MTR.1.1: | Actively participate in effortful learning both individually and collectively. Mathematicians who participate in effortful learning both individually and with others:
- Analyze the problem in a way that makes sense given the task.
- Ask questions that will help with solving the task.
- Build perseverance by modifying methods as needed while solving a challenging task.
- Stay engaged and maintain a positive mindset when working to solve tasks.
- Help and support each other when attempting a new method or approach.
Clarifications:
Teachers who encourage students to participate actively in effortful learning both individually and with others:
- Cultivate a community of growth mindset learners.
- Foster perseverance in students by choosing tasks that are challenging.
- Develop students’ ability to analyze and problem solve.
- Recognize students’ effort when solving challenging problems.
|
|
| MA.K12.MTR.2.1: | Demonstrate understanding by representing problems in multiple ways. Mathematicians who demonstrate understanding by representing problems in multiple ways: - Build understanding through modeling and using manipulatives.
- Represent solutions to problems in multiple ways using objects, drawings, tables, graphs and equations.
- Progress from modeling problems with objects and drawings to using algorithms and equations.
- Express connections between concepts and representations.
- Choose a representation based on the given context or purpose.
Clarifications:
Teachers who encourage students to demonstrate understanding by representing problems in multiple ways: - Help students make connections between concepts and representations.
- Provide opportunities for students to use manipulatives when investigating concepts.
- Guide students from concrete to pictorial to abstract representations as understanding progresses.
- Show students that various representations can have different purposes and can be useful in different situations.
|
|
| MA.K12.MTR.3.1: | Complete tasks with mathematical fluency. Mathematicians who complete tasks with mathematical fluency: - Select efficient and appropriate methods for solving problems within the given context.
- Maintain flexibility and accuracy while performing procedures and mental calculations.
- Complete tasks accurately and with confidence.
- Adapt procedures to apply them to a new context.
- Use feedback to improve efficiency when performing calculations.
Clarifications:
Teachers who encourage students to complete tasks with mathematical fluency:- Provide students with the flexibility to solve problems by selecting a procedure that allows them to solve efficiently and accurately.
- Offer multiple opportunities for students to practice efficient and generalizable methods.
- Provide opportunities for students to reflect on the method they used and determine if a more efficient method could have been used.
|
|
| MA.K12.MTR.4.1: | Engage in discussions that reflect on the mathematical thinking of self and others. Mathematicians who engage in discussions that reflect on the mathematical thinking of self and others: - Communicate mathematical ideas, vocabulary and methods effectively.
- Analyze the mathematical thinking of others.
- Compare the efficiency of a method to those expressed by others.
- Recognize errors and suggest how to correctly solve the task.
- Justify results by explaining methods and processes.
- Construct possible arguments based on evidence.
Clarifications:
Teachers who encourage students to engage in discussions that reflect on the mathematical thinking of self and others:- Establish a culture in which students ask questions of the teacher and their peers, and error is an opportunity for learning.
- Create opportunities for students to discuss their thinking with peers.
- Select, sequence and present student work to advance and deepen understanding of correct and increasingly efficient methods.
- Develop students’ ability to justify methods and compare their responses to the responses of their peers.
|
|
| MA.K12.MTR.5.1: | Use patterns and structure to help understand and connect mathematical concepts. Mathematicians who use patterns and structure to help understand and connect mathematical concepts: - Focus on relevant details within a problem.
- Create plans and procedures to logically order events, steps or ideas to solve problems.
- Decompose a complex problem into manageable parts.
- Relate previously learned concepts to new concepts.
- Look for similarities among problems.
- Connect solutions of problems to more complicated large-scale situations.
Clarifications:
Teachers who encourage students to use patterns and structure to help understand and connect mathematical concepts:- Help students recognize the patterns in the world around them and connect these patterns to mathematical concepts.
- Support students to develop generalizations based on the similarities found among problems.
- Provide opportunities for students to create plans and procedures to solve problems.
- Develop students’ ability to construct relationships between their current understanding and more sophisticated ways of thinking.
|
|
| MA.K12.MTR.6.1: | Assess the reasonableness of solutions. Mathematicians who assess the reasonableness of solutions: - Estimate to discover possible solutions.
- Use benchmark quantities to determine if a solution makes sense.
- Check calculations when solving problems.
- Verify possible solutions by explaining the methods used.
- Evaluate results based on the given context.
Clarifications:
Teachers who encourage students to assess the reasonableness of solutions:- Have students estimate or predict solutions prior to solving.
- Prompt students to continually ask, “Does this solution make sense? How do you know?”
- Reinforce that students check their work as they progress within and after a task.
- Strengthen students’ ability to verify solutions through justifications.
|
|
| MA.K12.MTR.7.1: | Apply mathematics to real-world contexts. Mathematicians who apply mathematics to real-world contexts: - Connect mathematical concepts to everyday experiences.
- Use models and methods to understand, represent and solve problems.
- Perform investigations to gather data or determine if a method is appropriate.
• Redesign models and methods to improve accuracy or efficiency.
Clarifications:
Teachers who encourage students to apply mathematics to real-world contexts:- Provide opportunities for students to create models, both concrete and abstract, and perform investigations.
- Challenge students to question the accuracy of their models and methods.
- Support students as they validate conclusions by comparing them to the given situation.
- Indicate how various concepts can be applied to other disciplines.
|
|
| ELA.K12.EE.1.1: | Cite evidence to explain and justify reasoning.Clarifications:
K-1 Students include textual evidence in their oral communication with guidance and support from adults. The evidence can consist of details from the text without naming the text. During 1st grade, students learn how to incorporate the evidence in their writing.2-3 Students include relevant textual evidence in their written and oral communication. Students should name the text when they refer to it. In 3rd grade, students should use a combination of direct and indirect citations. 4-5 Students continue with previous skills and reference comments made by speakers and peers. Students cite texts that they’ve directly quoted, paraphrased, or used for information. When writing, students will use the form of citation dictated by the instructor or the style guide referenced by the instructor. 6-8 Students continue with previous skills and use a style guide to create a proper citation. 9-12 Students continue with previous skills and should be aware of existing style guides and the ways in which they differ.
|
|
| ELA.K12.EE.2.1: | Read and comprehend grade-level complex texts proficiently.Clarifications:
See Text Complexity for grade-level complexity bands and a text complexity rubric. |
|
| ELA.K12.EE.3.1: | Make inferences to support comprehension.Clarifications:
Students will make inferences before the words infer or inference are introduced. Kindergarten students will answer questions like “Why is the girl smiling?” or make predictions about what will happen based on the title page.
Students will use the terms and apply them in 2nd grade and beyond. |
|
| ELA.K12.EE.4.1: | Use appropriate collaborative techniques and active listening skills when engaging in discussions in a variety of situations.Clarifications:
In kindergarten, students learn to listen to one another respectfully.In grades 1-2, students build upon these skills by justifying what they are thinking. For example: “I think ________ because _______.” The collaborative conversations are becoming academic conversations. In grades 3-12, students engage in academic conversations discussing claims and justifying their reasoning, refining and applying skills. Students build on ideas, propel the conversation, and support claims and counterclaims with evidence.
|
|
| ELA.K12.EE.5.1: | Use the accepted rules governing a specific format to create quality work.Clarifications:
Students will incorporate skills learned into work products to produce quality work. For students to incorporate these skills appropriately, they must receive instruction. A 3rd grade student creating a poster board display must have instruction in how to effectively present information to do quality work. |
|
| ELA.K12.EE.6.1: | Use appropriate voice and tone when speaking or writing.Clarifications:
In kindergarten and 1st grade, students learn the difference between formal and informal language. For example, the way we talk to our friends differs from the way we speak to adults. In 2nd grade and beyond, students practice appropriate social and academic language to discuss texts. |
|
| ELD.K12.ELL.MA.1: | English language learners communicate information, ideas and concepts necessary for academic success in the content area of Mathematics. |

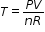 to isolate temperature as the quantity of interest.
to isolate temperature as the quantity of interest. 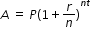 , solve for P.
, solve for P. 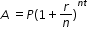 , solve for t.
, solve for t.
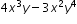 is equivalent to the factored form
is equivalent to the factored form 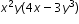 .
.
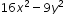 is equivalent to the factored form
is equivalent to the factored form
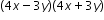 .
.
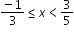 .
. 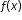
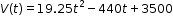 , where t is the number of years since 1972. In what year does the car’s value start to increase?
, where t is the number of years since 1972. In what year does the car’s value start to increase?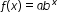 , where b is a whole number greater than 1 or a unit fraction, or
, where b is a whole number greater than 1 or a unit fraction, or 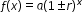 , where
, where 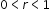 .
.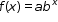 , where b is a whole number greater than 1 or a unit fraction or
, where b is a whole number greater than 1 or a unit fraction or 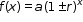 , where
, where 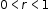 .
.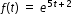 can be transformed into the straight line y=5t+2 by taking the natural logarithm of the function’s outputs.
can be transformed into the straight line y=5t+2 by taking the natural logarithm of the function’s outputs.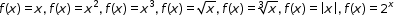 and
and 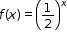 .
.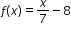 models Alicia’s position in miles relative to a water stand x minutes into a marathon. Evaluate and interpret for a quarter of an hour into the race.
models Alicia’s position in miles relative to a water stand x minutes into a marathon. Evaluate and interpret for a quarter of an hour into the race.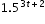 is equivalent to the expression
is equivalent to the expression 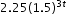 which is equivalent to
which is equivalent to 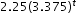 .
.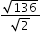 is equivalent to
is equivalent to 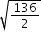 which is equivalent to
which is equivalent to 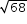 which is equivalent to
which is equivalent to 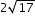 .
.