Access Point #: MAFS.912.G-CO.4.AP.12d Archived Access Point
Bisect an angle.
Clarifications:
Essential Understandings
Concrete:
- When given an angle, use manipulatives (e.g., compass, protractor, reflective devices, paper folding, dynamic geometric software, etc.) to bisect the given angle.
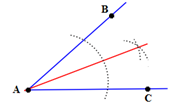
- Place point of compass on the vertex of
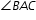 (point A).
(point A). - Stretch the compass to any length so long as it stays ON the angle.
- Swing an arc so the pencil crosses both sides of
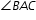 . This will create two intersection points with the sides (rays) of the angle.
. This will create two intersection points with the sides (rays) of the angle. - Place the compass point on one of these new intersection points on the sides of
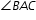 .
. - Without changing the width of the compass, place the point of the compass on the other intersection point on the side of the angle and make the same arc. The two small arcs in the interior of the angle should be crossing.
- Connect the point where the two small arcs cross to the vertex A of the angle.
- The two new angles created are of equal measure (and are each ½ the measure of
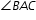 ).
).
- Bisect means to divide into two equal parts.
- MathisFun: Click Here
General Information
Number: MAFS.912.G-CO.4.AP.12d
Category: Access Points
Date Adopted or Revised: 07/14
Cluster: Make geometric constructions. (Geometry - Supporting Cluster) : Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.
This access point is part of these courses.
