MAFS.912.G-C.1.1Archived Standard

loading spinner
Export Print
Prove that all circles are similar.
General Information
Subject Area: Mathematics
Grade: 912
Domain-Subdomain: Geometry: Circles
Cluster: Level 2: Basic Application of Skills & Concepts
Cluster: Understand and apply theorems about circles. (Geometry - Additional Cluster) -

Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.

Date Adopted or Revised: 02/14
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 02/14
Status: State Board Approved - Archived
Assessed: Yes
Test Item Specifications

  • Assessment Limits :
    Items should not require the student to use the distance or midpoint
    formula.

    Items should not require the student to write an equation of a circle.

    Items may require the student to be familiar with using the algebraic
    description (x,y) begin mathsize 12px style rightwards arrow end style(x+a,y+b) for a translation, and
     (x,y) begin mathsize 12px style rightwards arrow end style(kx,ky) for a dilation when given the center of dilation.

    Items may require the student to be familiar with the algebraic
    description for a 90-degree rotation about the origin,
     (x,y) begin mathsize 12px style rightwards arrow end style(-y,x), for a 180-degree rotation about the origin,
     (x,y) begin mathsize 12px style rightwards arrow end style(-x,-y) , and for a 270-degree rotation about the origin,
     (x,y) begin mathsize 12px style rightwards arrow end style(y,-x) . 

     

    Items that use more than one transformation may
    ask the student to write a series of algebraic descriptions.

    Items should not use matrices to describe transformations.

  • Calculator :

    Neutral

  • Clarification :

    Students will use a sequence of transformations to prove that circles
    are similar.

    Students will use the measures of different parts of a circle to
    determine similarity.

  • Stimulus Attributes :
    Circles should not be given in equation form.

    Items may be set in a real-world or mathematical context.
  • Response Attributes :
    Items may require the student to use or choose the correct unit of
    measure
Sample Test Items (1)
  • Test Item #: Sample Item 1
  • Question:

    Circle A has a center at the origin and a point D located on the circle at (1,0). Circle B has a center at (1,-2) and a point E located on the circle at (4,-2).

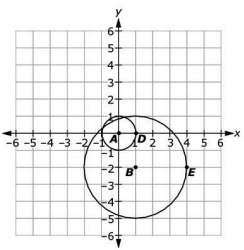
    Logan performs two transformations on circle A to show that circle A is similar to circle B.

    He first dilates the circle with the center of dilation at the origin and then translates the new circle.

    What are the algebraic descriptions of the two transformations?

  • Difficulty: N/A
  • Type: EE: Equation Editor

Related Courses

This benchmark is part of these courses.
1200400: Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206300: Informal Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated))
1206310: Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
1206320: Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7912060: Access Informal Geometry (Specifically in versions: 2014 - 2015 (course terminated))
1206315: Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 and beyond (current))
7912065: Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current))

Related Access Points

Alternate version of this benchmark for students with significant cognitive disabilities.

Related Resources

Vetted resources educators can use to teach the concepts and skills in this benchmark.

Formative Assessments

Similar Circles:

Students are given two circles with different radii and are asked to prove that the circles are similar.

Type: Formative Assessment

All Circles Are Similar:

Students are given two circles with different radius lengths and are asked to prove that the circles are similar.

Type: Formative Assessment

Lesson Plans

Why are Circles Similar?:

Students learn how to prove that all circles are similar using the three transformations (reflection, dilation, translation) on a unique circle. The lesson takes students through multiple-step transformations to show a proof of circle similarity. A Socratic discussion is used as closure to aid in the comprehension of circle similarity.

Type: Lesson Plan

Are All Circles Similar?:

This lesson allows students to prove that all circles are similar using transformations. Students will need prior knowledge of similarity, transformations, and the definition of a circle. The lesson begins with a warm up regarding dilations, then poses the question: Are all circles similar? The students are guided through the proof using a translation and dilation. The teacher emphasizes the details in the proof. The lesson closes with an exit ticket.

Type: Lesson Plan

Circle to Circle:

Students use coordinate based translations and dilations to prove circles are similar.

Type: Lesson Plan

Perspectives Video: Professional/Enthusiast

All Circles Are Similar- Especially Circular Pizza!:

What better way to demonstrate that all circles are similar then to use pizzas! Gaines Street Pies explains how all pizza pies are similar through transformations.

Download the CPALMS Perspectives video student note taking guide.

Type: Perspectives Video: Professional/Enthusiast

MFAS Formative Assessments

All Circles Are Similar:

Students are given two circles with different radius lengths and are asked to prove that the circles are similar.

Similar Circles:

Students are given two circles with different radii and are asked to prove that the circles are similar.

Student Resources

Vetted resources students can use to learn the concepts and skills in this benchmark.

Parent Resources

Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.