MAFS.912.G-CO.2.6Archived Standard

loading spinner
Export Print
Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.
General Information
Subject Area: Mathematics
Grade: 912
Domain-Subdomain: Geometry: Congruence
Cluster: Level 2: Basic Application of Skills & Concepts
Cluster: Understand congruence in terms of rigid motions. (Geometry - Major Cluster) -

Clusters should not be sorted from Major to Supporting and then taught in that order. To do so would strip the coherence of the mathematical ideas and miss the opportunity to enhance the major work of the grade with the supporting clusters.

Date Adopted or Revised: 02/14
Content Complexity Rating: Level 2: Basic Application of Skills & Concepts - More Information
Date of Last Rating: 02/14
Status: State Board Approved - Archived
Assessed: Yes
Test Item Specifications
    Also assesses:

    MAFS.912.G-CO.2.7

    MAFS.912.G-CO.2.8
  • Assessment Limits :
    Items may require the student to be familiar with using the algebraic
    description begin mathsize 12px style left parenthesis x comma y right parenthesis rightwards arrow left parenthesis x plus a comma y plus b right parenthesis end style for a translation, and
    begin mathsize 12px style left parenthesis x comma y right parenthesis rightwards arrow left parenthesis k x comma k y right parenthesis end style for a dilation when given the center of dilation.

    Items may require the student to be familiar with the algebraic
    description for a 90-degree rotation about the origin,
    begin mathsize 12px style left parenthesis x comma y right parenthesis rightwards arrow left parenthesis negative y comma x right parenthesis end style for a 180-degree rotation about the origin,
    begin mathsize 12px style left parenthesis x comma y right parenthesis rightwards arrow left parenthesis negative x comma negative y right parenthesis end style and for a 270-degree rotation about the origin,
    begin mathsize 12px style left parenthesis x comma y right parenthesis rightwards arrow left parenthesis y comma negative x right parenthesis end style . 

    Items that use more than one transformation may
    ask the student to write a series of algebraic descriptions.

    Items must not use matrices to describe transformations.

    Items must not require the student to use the distance formula.

    Items may require the student to find the distance between two
    points or the slope of a line.

    In items that require the student to represent transformations, at
    least two transformations should be applied

  • Calculator :

    Neutral

  • Clarification :
    Students will use rigid motions to transform figures.

    Students will predict the effect of a given rigid motion on a given
    figure.

    Students will use the definition of congruence in terms of rigid
    motions to determine if two figures are congruent.

    Students will explain triangle congruence using the definition of
    congruence in terms of rigid motions.

    Students will apply congruence to solve problems.

    Students will use congruence to justify steps within the context of a
    proof.

  • Stimulus Attributes :
    Items may be set in a real-world or mathematical context.

    Items may require the student to determine the rigid motions that
    show that two triangles are congruent.

  • Response Attributes :
    Items may ask the student to name corresponding angles and/or
    sides.

    Items may require the student to use a function, e.g.,

    y=k(f(x+a))+b , to describe a transformation.


    In items in which the student must write the line of reflection, any
    line may be used.

     

    Items may require the student to be familiar with slope-intercept
    form of a line, standard form of a line, and point-slope form of a line.

    Items may require the student to name corresponding angles or
    sides.

     

    Items may require the student to determine the transformations
    required to show a given congruence.

    Items may require the student to list sufficient conditions to prove
    triangles are congruent.

    Items may require the student to determine if given information is
    sufficient for congruence.

    Items may require the student to give statements to complete formal
    and informal proofs.



     

Sample Test Items (1)
  • Test Item #: Sample Item 1
  • Question:

    Evelyn is designing a pattern for a quilt using polygon EQFRGSHP shown.

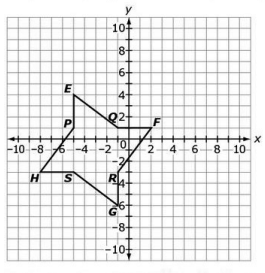
    Evelyn transforms EQFRGSHP so that the impage of E is at (2,0) and the image of R is at (6,-7). Which transformation could Evelyn have used to show EQFRGSHP and its image are congruent?

  • Difficulty: N/A
  • Type: MC: Multiple Choice

Related Courses

This benchmark is part of these courses.
1200400: Foundational Skills in Mathematics 9-12 (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
1206300: Informal Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022 (course terminated))
1206310: Geometry (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
1206320: Geometry Honors (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7912060: Access Informal Geometry (Specifically in versions: 2014 - 2015 (course terminated))
1206315: Geometry for Credit Recovery (Specifically in versions: 2014 - 2015, 2015 - 2022, 2022 - 2024, 2024 and beyond (current))
7912065: Access Geometry (Specifically in versions: 2015 - 2022, 2022 and beyond (current))

Related Access Points

Alternate version of this benchmark for students with significant cognitive disabilities.

Related Resources

Vetted resources educators can use to teach the concepts and skills in this benchmark.

Educational Software / Tool

Transformations Using Technology:

This virtual manipulative can be used to demonstrate and explore the effect of translation, rotation, and/or reflection on a variety of plane figures. A series of transformations can be explored to result in a specified final image.

Type: Educational Software / Tool

Formative Assessments

Congruent Trapezoids:

Students will determine whether two given trapezoids are congruent.

Type: Formative Assessment

Transform This:

Students are asked to translate and rotate a triangle in the coordinate plane and explain why the pre-image and image are congruent.

Type: Formative Assessment

Repeated Reflections and Rotations:

Students are asked to describe what happens to a triangle after repeated reflections and rotations.

Type: Formative Assessment

Lesson Plans

Coding Geometry Challenge #23 & 24:

This set of geometry challenges focuses on using transformations to show similarity and congruence of polygons and circles. Students problem solve and think as they learn to code using block coding software.  Student will need to use their knowledge of the attributes of polygons and mathematical principals of geometry to accomplish the given challenges. The challenges start out fairly simple and move to more complex situations in which students can explore at their own pace or work as a team. Computer Science standards are seamlessly intertwined with the math standards while providing “Step it up!” and “Jump it up!” opportunities to increase rigor.

Type: Lesson Plan

Where Will I Land?:

This is a beginning level lesson on predicting the effect of a series of reflections or a quick review of reflections for high school students.

Type: Lesson Plan

How do your Air Jordans move?:

In this inquiry lesson, students are moving their individually designed Air Jordans around the room to explore rigid transformations on their shoes. They will Predict-Observe-Explain the transformations and then have to explain their successes/failures to other students.

Type: Lesson Plan

Congruence vs. Similarity:

Students will learn the difference between congruence and similarity of classes of figures (such as circles, parallelograms) in terms of the number of variable lengths in the class. A third category will allow not only rigid motions and dilations, but also a single one-dimensional stretch, allowing more classes of figures to share sufficient common features to belong.

Type: Lesson Plan

Transformers 3:

Students will learn the vocabulary of three rigid transformations, reflection, translation, and rotation, and how they relate to congruence. Students will practice transforming figures by applying each isometry and identifying which transformation was used on a figure. The teacher will assign students to take pictures of the three transformations found in the real world.

Type: Lesson Plan

Problem-Solving Tasks

Reflections and Isosceles Triangles:

This activity uses rigid transformations of the plane to explore symmetries of classes of triangles.

Type: Problem-Solving Task

Reflections and Equilateral Triangles:

This activity is one in a series of tasks using rigid transformations of the plane to explore symmetries of classes of triangles, with this task in particular focusing on the class of equilaterial triangles

Type: Problem-Solving Task

Building a tile pattern by reflecting octagons:

This task applies reflections to a regular octagon to construct a pattern of four octagons enclosing a quadrilateral: the focus of the task is on using the properties of reflections to deduce that the quadrilateral is actually a square.

Type: Problem-Solving Task

Building a tile pattern by reflecting hexagons:

This task applies reflections to a regular hexagon to construct a pattern of six hexagons enclosing a seventh: the focus of the task is on using the properties of reflections to deduce this seven hexagon pattern.

Type: Problem-Solving Task

MFAS Formative Assessments

Congruent Trapezoids:

Students will determine whether two given trapezoids are congruent.

Repeated Reflections and Rotations:

Students are asked to describe what happens to a triangle after repeated reflections and rotations.

Transform This:

Students are asked to translate and rotate a triangle in the coordinate plane and explain why the pre-image and image are congruent.

Student Resources

Vetted resources students can use to learn the concepts and skills in this benchmark.

Educational Software / Tool

Transformations Using Technology:

This virtual manipulative can be used to demonstrate and explore the effect of translation, rotation, and/or reflection on a variety of plane figures. A series of transformations can be explored to result in a specified final image.

Type: Educational Software / Tool

Problem-Solving Tasks

Reflections and Isosceles Triangles:

This activity uses rigid transformations of the plane to explore symmetries of classes of triangles.

Type: Problem-Solving Task

Reflections and Equilateral Triangles:

This activity is one in a series of tasks using rigid transformations of the plane to explore symmetries of classes of triangles, with this task in particular focusing on the class of equilaterial triangles

Type: Problem-Solving Task

Building a tile pattern by reflecting octagons:

This task applies reflections to a regular octagon to construct a pattern of four octagons enclosing a quadrilateral: the focus of the task is on using the properties of reflections to deduce that the quadrilateral is actually a square.

Type: Problem-Solving Task

Building a tile pattern by reflecting hexagons:

This task applies reflections to a regular hexagon to construct a pattern of six hexagons enclosing a seventh: the focus of the task is on using the properties of reflections to deduce this seven hexagon pattern.

Type: Problem-Solving Task

Parent Resources

Vetted resources caregivers can use to help students learn the concepts and skills in this benchmark.

Problem-Solving Tasks

Reflections and Isosceles Triangles:

This activity uses rigid transformations of the plane to explore symmetries of classes of triangles.

Type: Problem-Solving Task

Reflections and Equilateral Triangles:

This activity is one in a series of tasks using rigid transformations of the plane to explore symmetries of classes of triangles, with this task in particular focusing on the class of equilaterial triangles

Type: Problem-Solving Task

Building a tile pattern by reflecting octagons:

This task applies reflections to a regular octagon to construct a pattern of four octagons enclosing a quadrilateral: the focus of the task is on using the properties of reflections to deduce that the quadrilateral is actually a square.

Type: Problem-Solving Task

Building a tile pattern by reflecting hexagons:

This task applies reflections to a regular hexagon to construct a pattern of six hexagons enclosing a seventh: the focus of the task is on using the properties of reflections to deduce this seven hexagon pattern.

Type: Problem-Solving Task