Multiplying Polynomials - 1

Getting Started

The student is not able to correctly multiply the polynomials and is unable to determine or explain that the polynomials are closed for multiplication.

The student:

• Does not correctly distribute.
  
  
  
  
  
  
  
  
• Multiplies the expressions partially or fully, but then combines terms that are not like or adds exponents.
  
  
  
  
  
  
  
  
  
  
  
  

What does it mean to distribute?

How did you multiply the monomial and the binomial?

How did you multiply the binomial and the trinomial?

There is an error in your multiplication; can you find it?

When you multiply , what is the product?

Review the application of the Distributive Property with the student. Model the use of the Distributive Property and provide additional examples for the student to complete, ensuring that at least some examples require distributing a negative value over sums and differences.

When multiplying a trinomial by a binomial, guide the student in identifying each pair of terms to be multiplied. Explain that the Distributive Property is used multiple times and model writing out the pairs of terms to be multiplied in a systematic and organized way. Remind the student that the problem can also be organized in a vertical fashion before multiplying. Assist the student in showing the work clearly so like terms can be identified, collected, and combined. Remind the student to write the final product in standard form. Provide additional similar multiplication problems for the student to complete.

Once the student is proficient multiplying polynomials, review the concept of closure of the integers under addition, subtraction, and multiplication. Then introduce the concept of closure of the polynomials under addition, subtraction, and multiplication.

Making Progress

The student correctly multiplies the polynomials but is unable to adequately explain that the polynomials are closed for multiplication.

The student answers one question positively and one negatively or both negatively (questions 3 and 4). The student does not demonstrate an understanding of a polynomial.

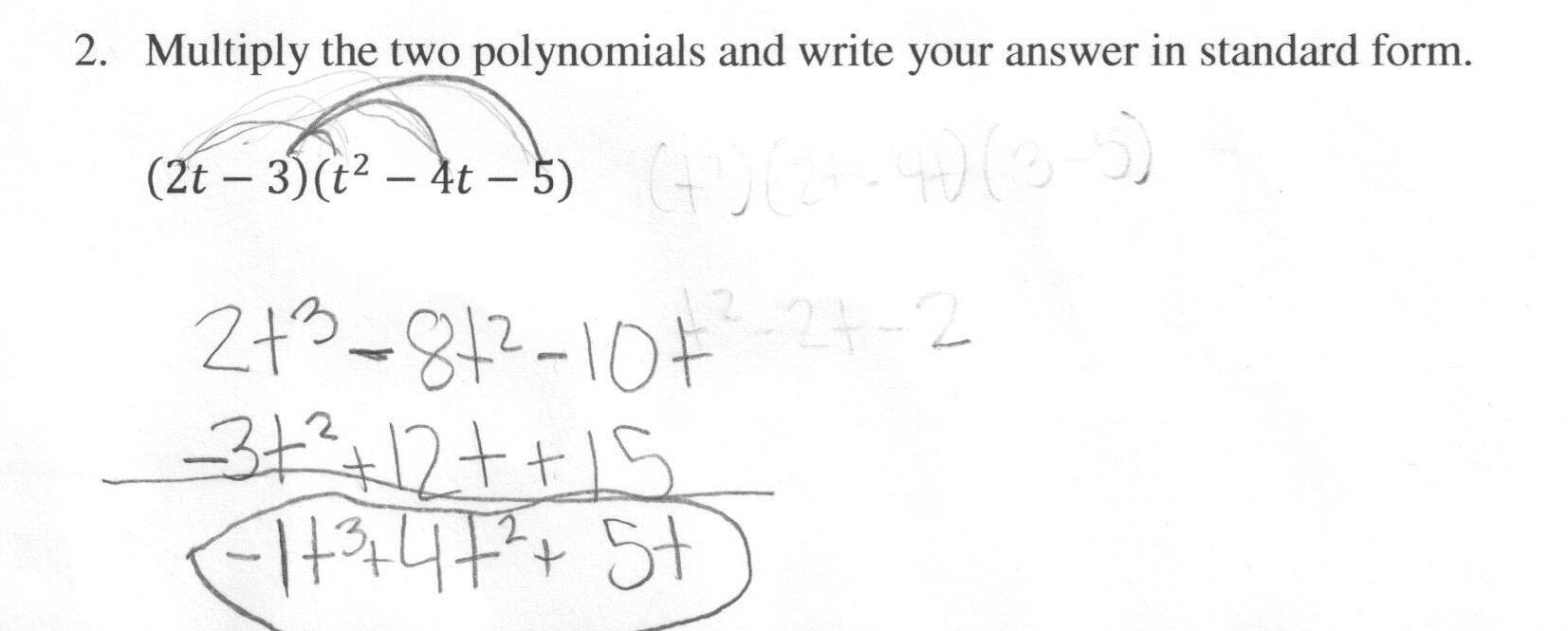
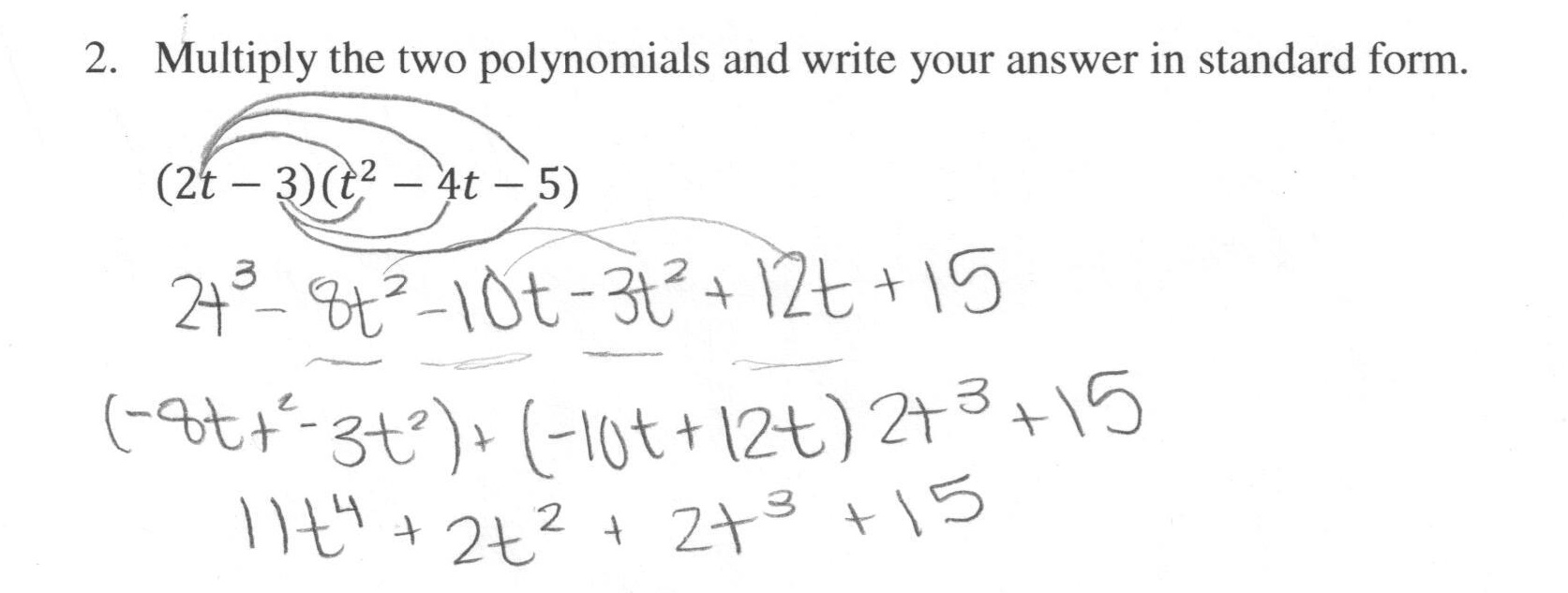
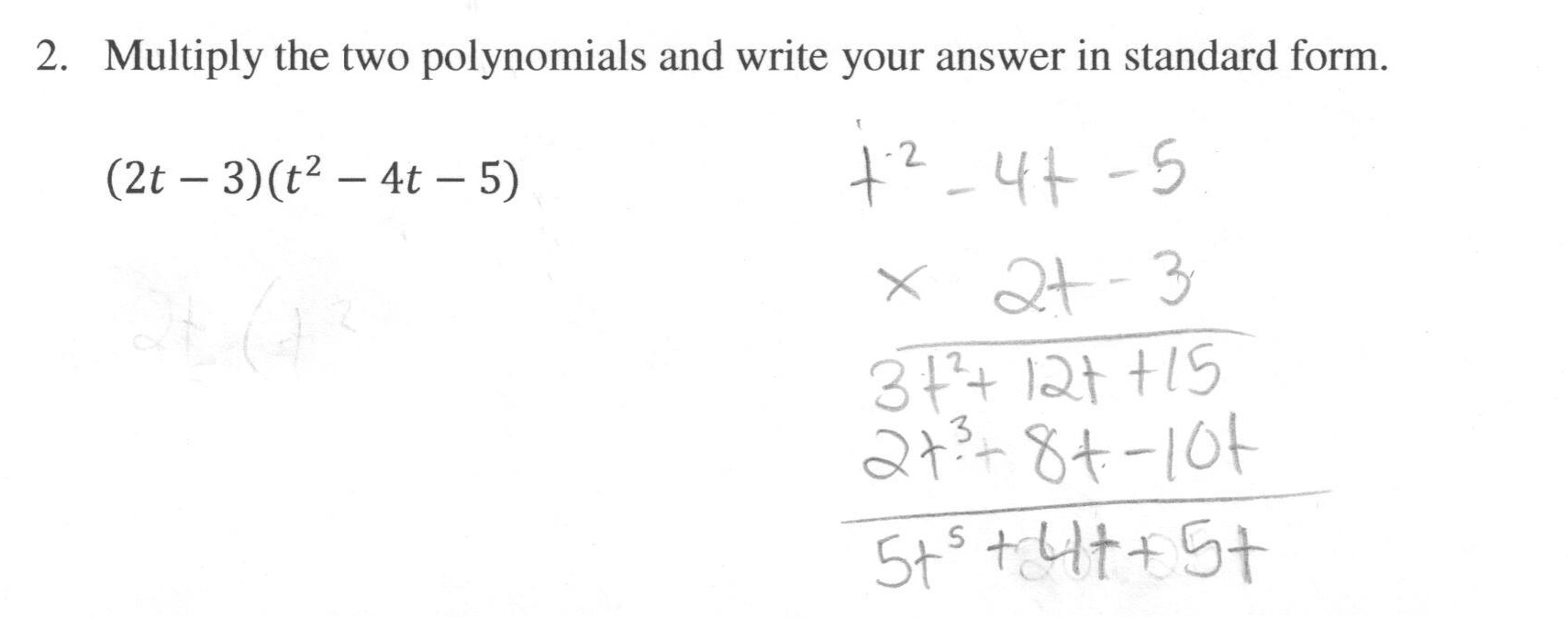
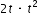The student answers both questions (3 and 4) positively, but cannot explain why the products are polynomials.

What is a polynomial?

What must be true of the terms of a polynomial? What do they look like?

Can you give me an example of an expression that is not a polynomial?

Is the expression 0 a polynomial?

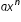Review the definition of a polynomial as the sum or difference of terms of the form where a is a real number and n is a whole number. The prefix poly can be misleading since a polynomial may have only one term which could be a constant, including zero. Provide additional examples and non-examples of polynomials (e.g., 0, 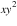, , 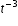3, y - 9,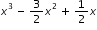). Ask the student to identify the examples of polynomials and explain why each non-example fails the definition.

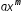Model explaining that for any two terms and 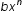(where a and b are real numbers and m and n are whole numbers), 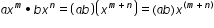. Since the real numbers are closed for multiplication, (a · b) is a real number. Since the whole numbers are closed for addition, (m + n) is a whole number. Therefore, multiplying terms of polynomials results in terms that fit the definition of a polynomial, [i.e., (a · b) is a real number and (m + n) is a whole number].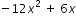

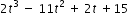
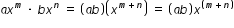Consider implementing MFAS tasks Adding Polynomials, Subtracting Polynomials, and Multiplying Polynomials - 2 to further assess the student"s understanding of the closure of the polynomials under addition, subtraction, and multiplication. 

Got It

The student provides complete and correct responses to all components of the task.

The student responds as follows to the four questions:

1. 
2. 
3. The student explains that is a polynomial since it consists of the sum of two terms each of the form where a is a real number and n is a whole number. Likewise, is a polynomial since the coefficients are real numbers for each term and all of the exponents are whole numbers.
4. The student further explains that the product of two polynomials will always be a polynomial because the result of multiplying terms of the form results in more terms of the form . The student may show that for any two terms and (where a and b are real numbers and m and n are whole numbers), . Since the real numbers are closed for multiplication, (a · b) is a real number. Since the whole numbers are closed for multiplication (m + n) is a whole number. Therefore, multiplying terms of polynomials results in terms that fit the definition of a polynomial. 

When you add or subtract two polynomials, will the result always be a polynomial?

When you divide two polynomials, will the result always be a polynomial?

Challenge the student to find an example of an operation with two polynomials that will result in an expression that is not a polynomial.

Consider implementing MFAS tasks Adding Polynomials, Subtracting Polynomials, and Multiplying Polynomials - 2 to further assess the student"s understanding of the closure of the polynomials under addition, subtraction, and multiplication.