| Name |
Description |
| MA.4.AR.1.1: | Solve real-world problems involving multiplication and division of whole numbers including problems in which remainders must be interpreted within the context.Clarifications:
Clarification 1: Problems involving multiplication include multiplicative comparisons. Refer to Situations Involving Operations with Numbers (Appendix A).
Clarification 2: Depending on the context, the solution of a division problem with a remainder may be the whole number part of the quotient, the whole number part of the quotient with the remainder, the whole number part of the quotient plus 1, or the remainder. Clarification 3: Multiplication is limited to products of up to 3 digits by 2 digits. Division is limited to up to 4 digits divided by 1 digit.
|
Examples:
A group of 243 students is taking a field trip and traveling in vans. If each van can hold 8 students, then the group would need 31 vans for their field trip because 243 divided by 8 equals 30 with a remainder of 3. |
|
| MA.4.AR.1.2: | Solve real-world problems involving addition and subtraction of fractions with like denominators, including mixed numbers and fractions greater than one.Clarifications:
Clarification 1: Problems include creating real-world situations based on an equation or representing a real-world problem with a visual model or equation.
Clarification 2: Fractions within problems must reference the same whole.
Clarification 3: Within this benchmark, the expectation is not to simplify or use lowest terms. Clarification 4: Denominators limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
|
Examples:
Example: Megan is making pies and uses the equation 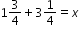 when baking. Describe a situation that can represent this equation. when baking. Describe a situation that can represent this equation.
Example: Clay is running a 10K race. So far, he has run 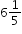 kilometers. How many kilometers does he have remaining? kilometers. How many kilometers does he have remaining?
|
|
| MA.4.AR.1.3: | Solve real-world problems involving multiplication of a fraction by a whole number or a whole number by a fraction.Clarifications:
Clarification 1: Problems include creating real-world situations based on an equation or representing a real-world problem with a visual model or equation.
Clarification 2: Fractions within problems must reference the same whole.
Clarification 3: Within this benchmark, the expectation is not to simplify or use lowest terms. Clarification 4: Fractions limited to fractions less than one with denominators of 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
|
Examples:
Ken is filling his garden containers with a cup that holds 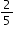 pounds of soil. If he uses 8 cups to fill his garden containers, how many pounds of soil did Ken use? pounds of soil. If he uses 8 cups to fill his garden containers, how many pounds of soil did Ken use? |
|
| MA.4.AR.2.1: | Determine and explain whether an equation involving any of the four operations with whole numbers is true or false.Clarifications:
Clarification 1: Multiplication is limited to whole number factors within 12 and related division facts. |
Examples:
The equation 32÷8=32-8-8-8-8 can be determined to be false because the expression on the left side of the equal sign is not equivalent to the expression on the right side of the equal sign. |
|
| MA.4.AR.2.2: | Given a mathematical or real-world context, write an equation involving multiplication or division to determine the unknown whole number with the unknown in any position.Clarifications:
Clarification 1: Instruction extends the development of algebraic thinking skills where the symbolic representation of the unknown uses a letter.
Clarification 2: Problems include the unknown on either side of the equal sign. Clarification 3: Multiplication is limited to factors within 12 and related division facts.
|
Examples:
The equation 96=8×t can be used to determine the cost of each movie ticket at the movie theatre if a total of $96 was spent on 8 equally priced tickets. Then each ticket costs $12. |
|
| MA.4.AR.3.1: | Determine factor pairs for a whole number from 0 to 144. Determine whether a whole number from 0 to 144 is prime, composite or neither.Clarifications:
Clarification 1: Instruction includes the connection to the relationship between multiplication and division and patterns with divisibility rules.
Clarification 2: The numbers 0 and 1 are neither prime nor composite.
|
|
| MA.4.AR.3.2: | Generate, describe and extend a numerical pattern that follows a given rule.Clarifications:
Clarification 1: Instruction includes patterns within a mathematical or real-world context. |
Examples:
Generate a pattern of four numbers that follows the rule of adding 14 starting at 5. |
|
| MA.4.DP.1.1: | Collect and represent numerical data, including fractional values, using tables, stem-and-leaf plots or line plots.Clarifications:
Clarification 1: Denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100. |
Examples:
A softball team is measuring their hat size. Each player measures the distance around their head to the nearest half inch. The data is collected and represented on a line plot. |
|
| MA.4.DP.1.2: | Determine the mode, median or range to interpret numerical data including fractional values, represented with tables, stem-and-leaf plots or line plots.Clarifications:
Clarification 1: Instruction includes interpreting data within a real-world context.
Clarification 2: Instruction includes recognizing that data sets can have one mode, no mode or more than one mode.
Clarification 3: Within this benchmark, data sets are limited to an odd number when calculating the median.
Clarification 4: Denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
|
Examples:
Given the data of the softball team’s hat size represented on a line plot, determine the most common size and the difference between the largest and the smallest sizes. |
|
| MA.4.DP.1.3: | Solve real-world problems involving numerical data.Clarifications:
Clarification 1: Instruction includes using any of the four operations to solve problems.
Clarification 2: Data involving fractions with like denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100. Fractions can be greater than one. Clarification 3: Data involving decimals are limited to hundredths.
|
Examples:
Given the data of the softball team’s hat size represented on a line plot, determine the fraction of the team that has a head size smaller than 20 inches. |
|
| MA.4.FR.1.1: | Model and express a fraction, including mixed numbers and fractions greater than one, with the denominator 10 as an equivalent fraction with the denominator 100.Clarifications:
Clarification 1: Instruction emphasizes conceptual understanding through the use of manipulatives, visual models, number lines or equations. |
|
| MA.4.FR.1.2: | Use decimal notation to represent fractions with denominators of 10 or 100, including mixed numbers and fractions greater than 1, and use fractional notation with denominators of 10 or 100 to represent decimals.Clarifications:
Clarification 1: Instruction emphasizes conceptual understanding through the use of manipulatives visual models, number lines or equations.
Clarification 2: Instruction includes the understanding that a decimal and fraction that are equivalent represent the same point on the number line and that fractions with denominators of 10 or powers of 10 may be called decimal fractions.
|
|
| MA.4.FR.1.3: | Identify and generate equivalent fractions, including fractions greater than one. Describe how the numerator and denominator are affected when the equivalent fraction is created.Clarifications:
Clarification 1: Instruction includes the use of manipulatives, visual models, number lines or equations.
Clarification 2: Instruction includes recognizing how the numerator and denominator are affected when equivalent fractions are generated.
|
|
| MA.4.FR.1.4: | Plot, order and compare fractions, including mixed numbers and fractions greater than one, with different numerators and different denominators.Clarifications:
Clarification 1: When comparing fractions, instruction includes using an appropriately scaled number line and using reasoning about their size.
Clarification 2: Instruction includes using benchmark quantities, such as 0, 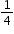 , , 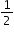 , , 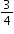 and 1, to compare fractions. and 1, to compare fractions.
Clarification 3: Denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
Clarification 4: Within this benchmark, the expectation is to use symbols (<, > or =).
|
Examples:
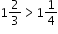 because because 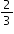 is greater than is greater than 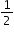 and and 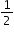 is greater than is greater than 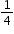 . . |
|
| MA.4.FR.2.1: | Decompose a fraction, including mixed numbers and fractions greater than one, into a sum of fractions with the same denominator in multiple ways. Demonstrate each decomposition with objects, drawings and equations.Clarifications:
Clarification 1: Denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100. |
Examples:
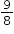 can be decomposed as can be decomposed as 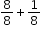 or as or as 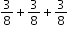 . . |
|
| MA.4.FR.2.2: | Add and subtract fractions with like denominators, including mixed numbers and fractions greater than one, with procedural reliability.Clarifications:
Clarification 1: Instruction includes the use of word form, manipulatives, drawings, the properties of operations or number lines.
Clarification 2: Within this benchmark, the expectation is not to simplify or use lowest terms. Clarification 3: Denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
|
Examples:
The difference 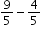 can be expressed as 9 fifths minus 4 fifths which is 5 fifths, or one. can be expressed as 9 fifths minus 4 fifths which is 5 fifths, or one. |
|
| MA.4.FR.2.3: | Explore the addition of a fraction with denominator of 10 to a fraction with denominator of 100 using equivalent fractions.Clarifications:
Clarification 1: Instruction includes the use of visual models.
Clarification 2: Within this benchmark, the expectation is not to simplify or use lowest terms.
|
Examples:
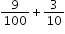 is equivalent to is equivalent to 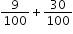 which is equivalent to which is equivalent to 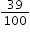 . . |
|
| MA.4.FR.2.4: | Extend previous understanding of multiplication to explore the multiplication of a fraction by a whole number or a whole number by a fraction.Clarifications:
Clarification 1: Instruction includes the use of visual models or number lines and the connection to the commutative property of multiplication. Refer to Properties of Operation, Equality and Inequality (Appendix D).
Clarification 2: Within this benchmark, the expectation is not to simplify or use lowest terms. Clarification 3: Fractions multiplied by a whole number are limited to less than 1. All denominators are limited to 2, 3, 4, 5, 6, 8, 10, 12, 16, 100.
|
|
| MA.4.GR.1.1: | Informally explore angles as an attribute of two-dimensional figures. Identify and classify angles as acute, right, obtuse, straight or reflex.Clarifications:
Clarification 1: Instruction includes classifying angles using benchmark angles of 90° and 180° in two-dimensional figures.
Clarification 2: When identifying angles, the expectation includes two-dimensional figures and real-world pictures.
|
|
| MA.4.GR.1.2: | Estimate angle measures. Using a protractor, measure angles in whole-number degrees and draw angles of specified measure in whole-number degrees. Demonstrate that angle measure is additive.Clarifications:
Clarification 1: Instruction includes measuring given angles and drawing angles using protractors.
Clarification 2: Instruction includes estimating angle measures using benchmark angles (30°, 45°, 60°, 90° and 180°).
Clarification 3: Instruction focuses on the understanding that angles can be decomposed into non-overlapping angles whose measures sum to the measure of the original angle.
|
|
| MA.4.GR.1.3: | Solve real-world and mathematical problems involving unknown whole-number angle measures. Write an equation to represent the unknown.Clarifications:
Clarification 1: Instruction includes the connection to angle measure as being additive. |
Examples:
A 60° angle is decomposed into two angles, one of which is 25°. What is the measure of the other angle? |
|
| MA.4.GR.2.1: | Solve perimeter and area mathematical and real-world problems, including problems with unknown sides, for rectangles with whole-number side lengths.Clarifications:
Clarification 1: Instruction extends the development of algebraic thinking where the symbolic representation of the unknown uses a letter.
Clarification 2: Problems involving multiplication are limited to products of up to 3 digits by 2 digits. Problems involving division are limited to up to 4 digits divided by 1 digit.
Clarification 3: Responses include the appropriate units in word form.
|
|
| MA.4.GR.2.2: | Solve problems involving rectangles with the same perimeter and different areas or with the same area and different perimeters.Clarifications:
Clarification 1: Instruction focuses on the conceptual understanding of the relationship between perimeter and area.
Clarification 2: Within this benchmark, rectangles are limited to having whole-number side lengths.
Clarification 3: Problems involving multiplication are limited to products of up to 3 digits by 2 digits. Problems involving division are limited to up to 4 digits divided by 1 digit.
Clarification 4: Responses include the appropriate units in word form.
|
Examples:
Possible dimensions of a rectangle with an area of 24 square feet include 6 feet by 4 feet or 8 feet by 3 feet. This can be found by cutting a rectangle into unit squares and rearranging them. |
|
| MA.4.M.1.1: | Select and use appropriate tools to measure attributes of objects.Clarifications:
Clarification 1: Attributes include length, volume, weight, mass and temperature.
Clarification 2: Instruction includes digital measurements and scales that are not linear in appearance. Clarification 3: When recording measurements, use fractions and decimals where appropriate.
|
|
| MA.4.M.1.2: | Convert within a single system of measurement using the units: yards, feet, inches; kilometers, meters, centimeters, millimeters; pounds, ounces; kilograms, grams; gallons, quarts, pints, cups; liter, milliliter; and hours, minutes, seconds.Clarifications:
Clarification 1: Instruction includes the understanding of how to convert from smaller to larger units or from larger to smaller units.
Clarification 2: Within the benchmark, the expectation is not to convert from grams to kilograms, meters to kilometers or milliliters to liters.
Clarification 3: Problems involving fractions are limited to denominators of 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
|
Examples:
Example: If a ribbon is 11 yards 2 feet in length, how long is the ribbon in feet?
Example: A gallon contains 16 cups. How many cups are in 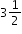 gallons? gallons?
|
|
| MA.4.M.2.1: | Solve two-step real-world problems involving distances and intervals of time using any combination of the four operations.Clarifications:
Clarification 1: Problems involving fractions will include addition and subtraction with like denominators and multiplication of a fraction by a whole number or a whole number by a fraction. Clarification 2: Problems involving fractions are limited to denominators of 2, 3, 4, 5, 6, 8, 10, 12, 16 and 100.
Clarification 3: Within the benchmark, the expectation is not to use decimals. |
|
| MA.4.M.2.2: | Solve one- and two-step addition and subtraction real-world problems involving money using decimal notation.
Examples:
Example: An item costs $1.84. If you give the cashier $2.00, how much change should you receive? What coins could be used to give the change?
Example: At the grocery store you spend $14.56. If you do not want any pennies in change, how much money could you give the cashier?
|
|
| MA.4.NSO.1.1: | Express how the value of a digit in a multi-digit whole number changes if the digit moves one place to the left or right. |
| MA.4.NSO.1.2: | Read and write multi-digit whole numbers from 0 to 1,000,000 using standard form, expanded form and word form.
Examples:
The number two hundred seventy-five thousand eight hundred two written in standard form is 275,802 and in expanded form is
200,000+70,000+5,000+800+2 or
(2×100,000)+(7×10,000)+(5×1,000)+(8×100)+(2×1). |
|
| MA.4.NSO.1.3: | Plot, order and compare multi-digit whole numbers up to 1,000,000.Clarifications:
Clarification 1: When comparing numbers, instruction includes using an appropriately scaled number line and using place values of the hundred thousands, ten thousands, thousands, hundreds, tens and ones digits.
Clarification 2: Scaled number lines must be provided and can be a representation of any range of numbers. Clarification 3: Within this benchmark, the expectation is to use symbols (<, > or =).
|
Examples:
The numbers 75,421; 74,241 and 74,521 can be arranged in ascending order as 74,241; 74,521 and 75,421. |
|
| MA.4.NSO.1.4: | Round whole numbers from 0 to 10,000 to the nearest 10, 100 or 1,000.
Examples:
Example: The number 6,325 is rounded to 6,300 when rounded to the nearest 100.
Example: The number 2,550 is rounded to 3,000 when rounded to the nearest 1,000.
|
|
| MA.4.NSO.1.5: | Plot, order and compare decimals up to the hundredths.Clarifications:
Clarification 1: When comparing numbers, instruction includes using an appropriately scaled number line and using place values of the ones, tenths and hundredths digits.
Clarification 2: Within the benchmark, the expectation is to explain the reasoning for the comparison and use symbols (<, > or =). Clarification 3: Scaled number lines must be provided and can be a representation of any range of numbers. |
Examples:
The numbers 3.2; 3.24 and 3.12 can be arranged in ascending order as 3.12; 3.2 and 3.24. |
|
| MA.4.NSO.2.1: | Recall multiplication facts with factors up to 12 and related division facts with automaticity. |
| MA.4.NSO.2.2: | Multiply two whole numbers, up to three digits by up to two digits, with procedural reliability.Clarifications:
Clarification 1: Instruction focuses on helping a student choose a method they can use reliably.
Clarification 2: Instruction includes the use of models or equations based on place value and the distributive property.
|
|
| MA.4.NSO.2.3: | Multiply two whole numbers, each up to two digits, including using a standard algorithm with procedural fluency. |
| MA.4.NSO.2.4: | Divide a whole number up to four digits by a one-digit whole number with procedural reliability. Represent remainders as fractional parts of the divisor.Clarifications:
Clarification 1: Instruction focuses on helping a student choose a method they can use reliably.
Clarification 2: Instruction includes the use of models based on place value, properties of operations or the relationship between multiplication and division.
|
|
| MA.4.NSO.2.5: | Explore the multiplication and division of multi-digit whole numbers using estimation, rounding and place value.Clarifications:
Clarification 1: Instruction focuses on previous understanding of multiplication with multiples of 10 and 100, and seeing division as a missing factor problem.
Clarification 2: Estimating quotients builds the foundation for division using a standard algorithm.
Clarification 3: When estimating the division of whole numbers, dividends are limited to up to four digits and divisors are limited to up to two digits.
|
Examples:
Example: The product of 215 and 460 can be estimated as being between 80,000 and 125,000 because it is bigger than 200×400 but smaller than 250×500.
Example: The quotient of 1,380 and 27 can be estimated as 50 because 27 is close to 30 and 1,380 is close to 1,500. 1,500 divided by 30 is the same as 150 tens divided by 3 tens which is 5 tens, or 50.
|
|
| MA.4.NSO.2.6: | Identify the number that is one-tenth more, one-tenth less, one-hundredth more and one-hundredth less than a given number.
Examples:
Example: One-hundredth less than 1.10 is 1.09.
Example: One-tenth more than 2.31 is 2.41.
|
|
| MA.4.NSO.2.7: | Explore the addition and subtraction of multi-digit numbers with decimals to the hundredths.Clarifications:
Clarification 1: Instruction includes the connection to money and the use of manipulatives and models based on place value. |
|
| MA.K12.MTR.1.1: | Actively participate in effortful learning both individually and collectively. Mathematicians who participate in effortful learning both individually and with others:
- Analyze the problem in a way that makes sense given the task.
- Ask questions that will help with solving the task.
- Build perseverance by modifying methods as needed while solving a challenging task.
- Stay engaged and maintain a positive mindset when working to solve tasks.
- Help and support each other when attempting a new method or approach.
Clarifications:
Teachers who encourage students to participate actively in effortful learning both individually and with others:
- Cultivate a community of growth mindset learners.
- Foster perseverance in students by choosing tasks that are challenging.
- Develop students’ ability to analyze and problem solve.
- Recognize students’ effort when solving challenging problems.
|
|
| MA.K12.MTR.2.1: | Demonstrate understanding by representing problems in multiple ways. Mathematicians who demonstrate understanding by representing problems in multiple ways: - Build understanding through modeling and using manipulatives.
- Represent solutions to problems in multiple ways using objects, drawings, tables, graphs and equations.
- Progress from modeling problems with objects and drawings to using algorithms and equations.
- Express connections between concepts and representations.
- Choose a representation based on the given context or purpose.
Clarifications:
Teachers who encourage students to demonstrate understanding by representing problems in multiple ways: - Help students make connections between concepts and representations.
- Provide opportunities for students to use manipulatives when investigating concepts.
- Guide students from concrete to pictorial to abstract representations as understanding progresses.
- Show students that various representations can have different purposes and can be useful in different situations.
|
|
| MA.K12.MTR.3.1: | Complete tasks with mathematical fluency. Mathematicians who complete tasks with mathematical fluency: - Select efficient and appropriate methods for solving problems within the given context.
- Maintain flexibility and accuracy while performing procedures and mental calculations.
- Complete tasks accurately and with confidence.
- Adapt procedures to apply them to a new context.
- Use feedback to improve efficiency when performing calculations.
Clarifications:
Teachers who encourage students to complete tasks with mathematical fluency:- Provide students with the flexibility to solve problems by selecting a procedure that allows them to solve efficiently and accurately.
- Offer multiple opportunities for students to practice efficient and generalizable methods.
- Provide opportunities for students to reflect on the method they used and determine if a more efficient method could have been used.
|
|
| MA.K12.MTR.4.1: | Engage in discussions that reflect on the mathematical thinking of self and others. Mathematicians who engage in discussions that reflect on the mathematical thinking of self and others: - Communicate mathematical ideas, vocabulary and methods effectively.
- Analyze the mathematical thinking of others.
- Compare the efficiency of a method to those expressed by others.
- Recognize errors and suggest how to correctly solve the task.
- Justify results by explaining methods and processes.
- Construct possible arguments based on evidence.
Clarifications:
Teachers who encourage students to engage in discussions that reflect on the mathematical thinking of self and others:- Establish a culture in which students ask questions of the teacher and their peers, and error is an opportunity for learning.
- Create opportunities for students to discuss their thinking with peers.
- Select, sequence and present student work to advance and deepen understanding of correct and increasingly efficient methods.
- Develop students’ ability to justify methods and compare their responses to the responses of their peers.
|
|
| MA.K12.MTR.5.1: | Use patterns and structure to help understand and connect mathematical concepts. Mathematicians who use patterns and structure to help understand and connect mathematical concepts: - Focus on relevant details within a problem.
- Create plans and procedures to logically order events, steps or ideas to solve problems.
- Decompose a complex problem into manageable parts.
- Relate previously learned concepts to new concepts.
- Look for similarities among problems.
- Connect solutions of problems to more complicated large-scale situations.
Clarifications:
Teachers who encourage students to use patterns and structure to help understand and connect mathematical concepts:- Help students recognize the patterns in the world around them and connect these patterns to mathematical concepts.
- Support students to develop generalizations based on the similarities found among problems.
- Provide opportunities for students to create plans and procedures to solve problems.
- Develop students’ ability to construct relationships between their current understanding and more sophisticated ways of thinking.
|
|
| MA.K12.MTR.6.1: | Assess the reasonableness of solutions. Mathematicians who assess the reasonableness of solutions: - Estimate to discover possible solutions.
- Use benchmark quantities to determine if a solution makes sense.
- Check calculations when solving problems.
- Verify possible solutions by explaining the methods used.
- Evaluate results based on the given context.
Clarifications:
Teachers who encourage students to assess the reasonableness of solutions:- Have students estimate or predict solutions prior to solving.
- Prompt students to continually ask, “Does this solution make sense? How do you know?”
- Reinforce that students check their work as they progress within and after a task.
- Strengthen students’ ability to verify solutions through justifications.
|
|
| MA.K12.MTR.7.1: | Apply mathematics to real-world contexts. Mathematicians who apply mathematics to real-world contexts: - Connect mathematical concepts to everyday experiences.
- Use models and methods to understand, represent and solve problems.
- Perform investigations to gather data or determine if a method is appropriate.
• Redesign models and methods to improve accuracy or efficiency.
Clarifications:
Teachers who encourage students to apply mathematics to real-world contexts:- Provide opportunities for students to create models, both concrete and abstract, and perform investigations.
- Challenge students to question the accuracy of their models and methods.
- Support students as they validate conclusions by comparing them to the given situation.
- Indicate how various concepts can be applied to other disciplines.
|
|
| ELA.K12.EE.1.1: | Cite evidence to explain and justify reasoning.Clarifications:
K-1 Students include textual evidence in their oral communication with guidance and support from adults. The evidence can consist of details from the text without naming the text. During 1st grade, students learn how to incorporate the evidence in their writing.2-3 Students include relevant textual evidence in their written and oral communication. Students should name the text when they refer to it. In 3rd grade, students should use a combination of direct and indirect citations. 4-5 Students continue with previous skills and reference comments made by speakers and peers. Students cite texts that they’ve directly quoted, paraphrased, or used for information. When writing, students will use the form of citation dictated by the instructor or the style guide referenced by the instructor. 6-8 Students continue with previous skills and use a style guide to create a proper citation. 9-12 Students continue with previous skills and should be aware of existing style guides and the ways in which they differ.
|
|
| ELA.K12.EE.2.1: | Read and comprehend grade-level complex texts proficiently.Clarifications:
See Text Complexity for grade-level complexity bands and a text complexity rubric. |
|
| ELA.K12.EE.3.1: | Make inferences to support comprehension.Clarifications:
Students will make inferences before the words infer or inference are introduced. Kindergarten students will answer questions like “Why is the girl smiling?” or make predictions about what will happen based on the title page.
Students will use the terms and apply them in 2nd grade and beyond. |
|
| ELA.K12.EE.4.1: | Use appropriate collaborative techniques and active listening skills when engaging in discussions in a variety of situations.Clarifications:
In kindergarten, students learn to listen to one another respectfully.In grades 1-2, students build upon these skills by justifying what they are thinking. For example: “I think ________ because _______.” The collaborative conversations are becoming academic conversations. In grades 3-12, students engage in academic conversations discussing claims and justifying their reasoning, refining and applying skills. Students build on ideas, propel the conversation, and support claims and counterclaims with evidence.
|
|
| ELA.K12.EE.5.1: | Use the accepted rules governing a specific format to create quality work.Clarifications:
Students will incorporate skills learned into work products to produce quality work. For students to incorporate these skills appropriately, they must receive instruction. A 3rd grade student creating a poster board display must have instruction in how to effectively present information to do quality work. |
|
| ELA.K12.EE.6.1: | Use appropriate voice and tone when speaking or writing.Clarifications:
In kindergarten and 1st grade, students learn the difference between formal and informal language. For example, the way we talk to our friends differs from the way we speak to adults. In 2nd grade and beyond, students practice appropriate social and academic language to discuss texts. |
|
| ELD.K12.ELL.MA.1: | English language learners communicate information, ideas and concepts necessary for academic success in the content area of Mathematics. |
| ELD.K12.ELL.SI.1: | English language learners communicate for social and instructional purposes within the school setting. |





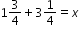 when baking. Describe a situation that can represent this equation.
when baking. Describe a situation that can represent this equation. 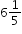 kilometers. How many kilometers does he have remaining?
kilometers. How many kilometers does he have remaining?
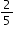 pounds of soil. If he uses 8 cups to fill his garden containers, how many pounds of soil did Ken use?
pounds of soil. If he uses 8 cups to fill his garden containers, how many pounds of soil did Ken use?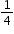 ,
, 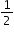 ,
, 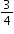 and 1, to compare fractions.
and 1, to compare fractions.
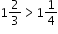 because
because 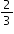 is greater than
is greater than 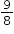 can be decomposed as
can be decomposed as 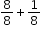 or as
or as 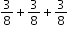 .
.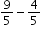 can be expressed as 9 fifths minus 4 fifths which is 5 fifths, or one.
can be expressed as 9 fifths minus 4 fifths which is 5 fifths, or one.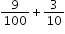 is equivalent to
is equivalent to 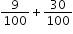 which is equivalent to
which is equivalent to 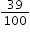 .
.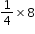 by imagining having 8 pizzas that she wants to split equally with three of her friends. She and each of her friends will get 2 pizzas since
by imagining having 8 pizzas that she wants to split equally with three of her friends. She and each of her friends will get 2 pizzas since 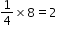 .
.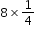 by imagining having 8 pizza boxes each with one-quarter slice of a pizza left. If she put them all together, she would have a total of 2 whole pizzas since
by imagining having 8 pizza boxes each with one-quarter slice of a pizza left. If she put them all together, she would have a total of 2 whole pizzas since 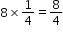 which is equivalent to 2.
which is equivalent to 2.
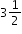 gallons?
gallons?